Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 53
Uma t��pica seção de parede de edifício é mostrada na Fig. P3–53.
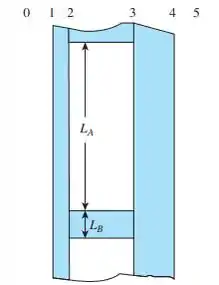
Esta seção se estende para dentro e para fora da parede e é repetida na direção vertical. Os membros de apoio de parede são feitos de aço e têm 8 cm . O restante do espaçamento interno da parede é preenchido com isolamento de medidas . A parede interna é feita com placas de gesso com e a parede externa é feita de tijolo com 10 cm de espessura . Qual é o fluxo médio de calor através dessa parede quando e ?
Passo 1
Muito bem galera, vamos pra mais uma!!
Antes de qualquer coisa nós vamos desenhar o que está acontecendo:
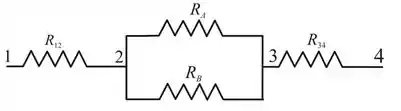
Legal, pelo esquema nós vemos que e estão em paralelo. Se é assim, podemos dizer que:
E esta resistência está em série com as demais, certo?
Então a resistência total será:
Vocês podem estar se perguntando: Mas por que não consideramos a resistência de 0 até 1 e de 4 até 5? Porque nós estamos considerando o fluxo do ponto 1 até o 4, ok?
Até aqui tudo certo !!
Passo 2
Agora vamos calcular cada resistência separadamente, ok? Para a área nós vamos vamos usar a altura, h, multiplicada pelo seu comprimento, w:
Legal! Agora, nós temos a altura e a espessura, mas não o comprimento.
O que fazemos então para achar a área? Vamos considera-lo unitário, ok?
Relembrando os dados:
E para todos:
E quanto a resistência total?
Substituindo
Com os dados que descobrimos:
Já achamos a resistência total, agora só precisamos do fluxo de calor!!
Passo 3
Se lembram de como calcular o calor?
Fácil, não é?
Substituindo:
Como a variação em graus Celsius é a mesma que a variação em kelvin:
Como estamos analisando um espaço referente a 0,605 m de comprimento e 1 m de largura:
Como a cada intervalo de 60,5 cm a estrutura da parede interna se repete nós temos que a cada metro quadrado existe uma troca de 49,9 W de calor.
E é isso aí galera !!