Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 58
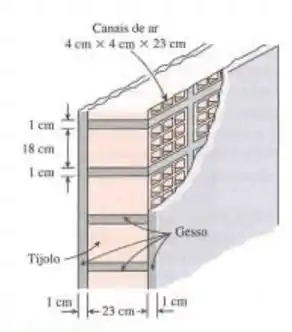
Uma parede de 25 cm de espessura, 9 m de comprimento e 3 m de altura deve ser construída com tijolos sólidos de ou tijolos de dimensões idênticas com nove buracos de ar que têm 23 cm de comprimento e seção transversal de . Existe uma camada de gesso de 1 cm de espessura entre dois tijolos adjacentes em todos os quatro lados e em ambos os lados da parede. A casa é mantida a 27°C, e a temperatura ambiente externa é de 2°C. Tomando os coeficientes de transferência de calor nas superfícies interna e externa da parede como sendo , respectivamente, determine a taxa de transferência de calor através da parede construída de
- Tijolos sólidos;
- Tijolos com orifícios de ar.
Passo 1
Respirem ai galera, porque vamos continuando !!
Na letra a nós assumimos que estes buracos não existam, certo? Então teremos em paralelo somente o gesso e o tijolo:
Nós temos o tijolo e o gesso, sendo assim, a estrutura da parede se repete a cada intervalo de Então a área representativa será:
Legal, pelo esquema nós vemos que e estão em paralelo entre si, então:
Que está em sequencia com as demais:
Até aqui tudo certo ?
Passo 2
Agora vamos calcular cada resistência separadamente, ok?
Relembrando os dados:
Agora vamos analisar as áreas que serão as diferentonas, tudo bem?
Em uma parte de gesso lateral nós teremos 19 cm de altura e 1 cm de comprimento:
A outra parte do gesso terá somente a altura do tijolo, 18 cm, e seu comprimento normal:
E a do tijolo:
Bom galera, já sabemos tudo o que precisamos:
E quanto a resistência total? Bora substituir né?
Já achamos a resistência total, agora só precisamos do fluxo de calor!!
Passo 3
Na letra b nós precisamos da taxa de transferência de calor pela parede.
Se lembram de como calcular o calor?
Fácil, não é?
Substituindo:
Como a variação em graus Celsius é a mesma que a variação em kelvin:
CCom relação à área representativa:
Como a cada intervalo de a estrutura da parede se repete, para a parede total de 9 m de comprimento e 3 m de altura a troca total de calor será:
Acharam que tinha acabado?
Nananinanão !! Falta a letra b
Passo 4
Na letra b nós ainda temos uma resistência a ser adicionada, não é?
A do ar! Sendo assim:
Aqui nós precisamos calcular a área dos orifícios, ok?
Se temos espaços vazios a área do tijolo também irá mudar:
Consequentemente mudamos a resistência do tijolo e adicionamos a dos orifícios:
E quanto a resistência total?
Bem diferente da anterior, não foi?
Passo 5
Bora lançar na fórmula do calor:
Com relação à área representativa:
Para a parede inteira:
Cansativa, não foi?
Mas acabamos !!