Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 161
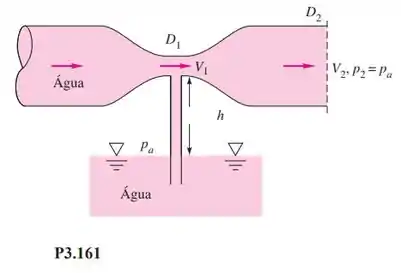
Um tubo convergente-divergente, chamado Venturi, desenvolve um escoamento de baixa pressão na garganta capaz de aspirar fluido para cima de um reservatório, como na Figura P3.161. Aplicando a equação de Bernoulli sem perdas, deduza uma expressão para a velocidade suficiente para começar a trazer fluido do reservatório para a garganta.
Passo 1
Essa questão pede basicamente para encontrarmos uma expressão para , então vamos utilizar a sempre útil equação de Bernoulli:
Antes de tudo bora esclarecer algumas coisas. Vamos escolher o nosso ponto 1 como um ponto na garganta do tubo de Venturi e o ponto 2 será um ponto na mesma altura que o ponto 1, ou seja, .
Para que o fluido do reservatório seja aspirado para cima, a pressão no reservatório () deve ser maior que a pressão na garganta do tubo. Sendo assim a pressão hidrostática mínima entre um ponto na garganta do tubo e um ponto no reservatório será:
Passo 2
Utilizando a equação da continuidade, vamos conseguir uma relação entre e :
Passo 3
Substituindo todas estas expressões na equação de Bernoulli e fazendo alguns ajustes vamos ter:
Ou seja, está é a expressão da velocidade mínima em 1 para que a água seja aspirada. Valores maiores que também irão aspirar o fluido.