Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 57

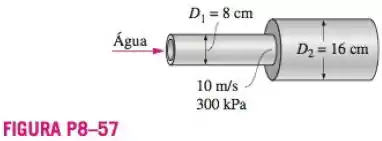
Um tubo horizontal tem uma expansão abrupta de D 1 = 8   c m para D 2 = 16   c m . A velocidade da água na seção menor é de 10   m / s e o escoamento é turbulento. A pressão na seção menor é de P 1 = 300   k P a . Tomando o fator de correção da energia cinética como 1,06 na entrada e na saída, determine a pressão a jusante P 2 e estime o erro que teria ocorrido se a equação de Bernoulli tivesse sido usada.

Passo 1

Temos que determinara a pressão de saída após uma abrupta expansão.

Para isto utilizaremos a equação do balanço energético para determinar pressão de saída, mas para podemos utilizar está equação, falta determinar a velocidade de saída, o coeficiente de perdas menores e a perda menor devido a esta expansão.

Assumindo que o fluxo é constante, horizontal, incompressível.

Temos a densidade da água como ρ = 1000   k g / m 3 .

Passo 2

Como dito anteriormente temos que determinar algumas coisas antes de utilizara equação do balanço, vamos determinar a velocidade de saída:

Como assumimos que o fluxo é constante e incompressível, pela conservação de massa, o fluxo de massa de entrada é o mesmo fluxo de massa de saída.

m ˙ 1 = m ˙ 2

A 1 ∙ ρ ∙ V 1 = A 2 ∙ ρ ∙ V 2

Isolando V 2 :

V 2 = A 1 A 2 ∙ V 1

V 2 = π D 1 2 4 π D 2 2 4 ∙ 10

V 2 = 0,08 2 0,16 2 ∙ 10 = 2,5   m / s

Passo 3

Vamos determinar o coeficiente de perda desta expansão abrupta.

O coeficiente da expansão é definido pela seguinte fórmula:

K L = α ∙ 1 - D 1 2 D 2 2 2

Como enunciado nos informou que o tipo de escoamento é turbulento, portanto, temos α = 1,05 , você pode conferir na tabela 8-4.

Substituindo valores:

K L = 1,05 ∙ 1 - 0,08 2 0,16 2 2 = 0,59

Temos o coeficiente de perda, podes determinar a perda de carga h L :

h L = K L ∙ V 1 2 2 g

h L = 0,59 ∙ 10 2 2 ∙ 9,81 = 3,01   m

Passo 4

Após todos nossos cálculos podemos utilizar a fórmula do balanço energético e determinar P 2 . Antes vamos deixar claro que devido o fluxo ser horizontal não possui diferenças de nível, portanto, z 1 = z 2 .

P 1 ρ g + α 1 V 1 2 g + z 1 + h b o m b a ,   u t = P 2 ρ g + α 2 V 2 2 2 g + z 2 + h t u r b i n a , e + h L

Simplificando a equação:

P 1 ρ g + α 1 ∙ V 1 2 2 g = P 2 ρ g + α 2 V 2 2 g + h L

Isolando P 2 :

P 2 = P 1 + ρ ∙ α 1 ∙ V 1 2 - α 2 ∙ V 2 2 2 - g h L

Substituindo valores:

P 2 = 300 ∙ 10 3 + 1000 ∙ 1,06 ∙ 10 2 - 1,06 ∙ 2,5 2 2 - 9,81 ∙ 3,01 = 320,1594   k P a

P 2 = 320,1594   k P a

Passo 5

Temos que estimar o erro que teria ocorrido se a equação de Bernoulli tivesse sido usada.

Equação de Bernoulli é definida por:

P 1 ρ g + V 1 2 g + z 1 = P 2 ρ g + V 2 2 2 g + z 2

Simplificando e isolando a pressão de saída:

P 1 ρ g + V 1 2 g = P 2 ρ g + V 2 2 2 g

P 2 = P 1 + ρ ∙ V 1 2 - V 2 2 2

Substituindo valores:

P 2 = 300 ∙ 10 3 + 1000 ∙ 10 2 - 2,5 2 2

P 2 = 346,875   k P a

Teríamos um erro de

e r r o = 346,875   k - 320,1594   k = 26,715   k P a

Em de erro percentual seria:

e r r o % = a p r o x i m a d o - e x a t o e x a t o

e r r o % = 346,875   k - 320,1594   k 320,1594   k = 0,08344 ≅ 8,3 %

Resposta

Pressão de saída:

P 2 = 320,1594   k P a

Pressão de saída com Bernoulli:

P 2 = 346,875   k P a

Erro percentual:

e r r o % = 8,3 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O efeito do arredondamento de uma saída de tubo sobre o coeficiente de perda é ( a ) desprezível, ( b ) um pouco significativo ou c muito significativo.
Um sistema de bombeamento envolve dois tubos de diâmetro diferentes (mas com comprimento, material e rugosidade iguais) conectados em série. Como você compara a as vazões e ( b ) as quedas de pressão
Um sistema de tubulação envolve dois tubos de diâmetro idênticos, mas com comprimentos diferentes conectados em paralelo. Como você compara as quedas de pressão desses dois tubos?
Durante um projeto de reajuste de um sistema de escoamento de fluido para reduzir a potência de bombeamento, é proposta a instalação de aletas nos cotovelos chanfrados, ou a substituição das curvas ag
O efeito do arredondamento de uma entrada de tubo sobre o coeficiente de perda é ( a ) desprezível, ( b ) um pouco significativo ou c muito significativo.