Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 54

Água deve ser retirada de um reservatório de água com 3   m de altura perfurando um orifício com 1,5   c m de diâmetro na superfície inferior. Desprezando o efeito do fator de correção da energia cinética, determine a vazão da água através do orifício se a a entrada do orifício for bem arredondada e b a entrada tiver arestas vivas.

Passo 1

Temos um tanque que está drenando água dele e temos que determinar a vazão da água pelo seu orifício para bem arredondada e arestas vivas.

Assumindo que o fluxo de água, é constante e incompressível, o reservatório estará aberto para atmosfera e como o enunciado pediu desprezando o efeito do fator de correção da energia cinética.

Temos a seguinte situação:

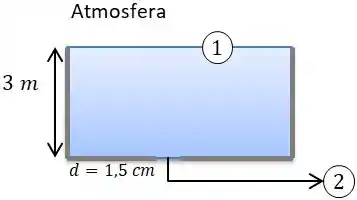
Você deve estar se perguntando oque são estes 1 e 2 , bem estes números são nossos pontos de nível, temos o nível z 2 = 0   m e z 1 = 3   m , estes pontos se encontram na superfície livre da água do tanque, ponto 1, e o outro na superfície livre da água na saída do orifício, ponto 2.

Como escolhemos dois pontos que se encontrar sobre influência da pressão atmosférica temos que P 1 = P 2 = P a t m .

A velocidade do fluido no ponto 1 será considerada zero devido à velocidade de drenagem comparada com a superfície é muito lenta, logo, pode assumir como zero.

Passo 2

Agora que determinamos todas as condições necessárias para determinar a velocidade de saída do orifício e por final a vazão, temos a equação do balanço energético como:

P 1 ρ g + α 1 V 1 2 g + z 1 + h b o m b a ,   u t = P 2 ρ g + α 2 V 2 2 2 g + z 2 + h t u r b i n a , e + h L

Simplificando a equação, temos:

z 1 = α 2 ∙ V 2 2 2 g + h L

Nesta equação nós falta determinar h L .

Passo 3

Temos que h L é definido por:

h L = K L V 2 2 2 g

Substituindo na equação do balanço:

z 1 = α 2 ∙ V 2 2 2 g + K L V 2 2 2 g

Simplificando a equação e isolando V 2 :

z 1 ∙ 2 g = α 2 V 2 2 + K L V 2 2

z 1 ∙ 2 g = ( α 2 + K L ) V 2 2

z 1 ∙ 2 g α 2 + K L = V 2 2

V 2 = z 1 ∙ 2 g α 2 + K L

Passo 4

a)Calculando a vazão de saída para entrada do orifício for bem arredondada:

Consultando a tabela 8-4, página 303, para bem arredondada K L = 0,03 .

Substituindo valores na fórmula da velocidade:

V 2 = 3 ∙ 2 ∙ 9,81 1 + 0,03

V 2 = 7,56   m / s

Temos que vazão volumétrica é definida por:

V ˙ = A ∙ V 2

V ˙ = π d 2 4 ∙ V 2

V ˙ = π 0,015 2 4 ∙ 7,56 = 1,335 ∙ 10 - 3   m 3 / s

Passo 5

b) executando os mesmo cálculos no passo 4 para a entrada tiver arestas vivas.

Consultando a tabela 8-4, página 303, arestas vivas K L = 0 , 5 .

Substituindo valores na fórmula da velocidade:

V 2 = 3 ∙ 2 ∙ 9,81 1 + 0,5

V 2 = 6,264   m / s

Temos que vazão volumétrica é definida por:

V ˙ = A ∙ V 2

V ˙ = π d 2 4 ∙ V 2

V ˙ = π 0,015 2 4 ∙ 6,264 = 1 , 1069 ∙ 10 - 3   m 3 / s

Resposta

a)   V ˙ = 1,335 ∙ 10 - 3   m 3 / s

b)   V ˙ = 1,1069 ∙ 10 - 3   m 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Defina o comprimento equivalente da perda menor no escoamento de tubo. Como ela se relaciona ao coeficiente de perda menor?
Um sistema de tubos envolve curvas agudas e, portanto, grandes perdas de carga menores. Uma forma de reduzir a perda de carga seria substituir as curvas agudas por cotovelos circulares. Qual seria a o
Um sistema de tubulação envolve dois tubos de diâmetro diferentes (mas com comprimento, material e rugosidade iguais) conectados em paralelo. Como você compara a as vazões e b as quedas de pressão nes
O que é perda menor em escoamento de tubo? Como é definido o coeficiente de perda menor K L ?
A água é bombeada de um grande reservatório mais baixo para um reservatório mais alto. Alguém afirma que se a perda de carga for desprezível, a carga de bomba necessária será igual à diferença de elev