Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 8.Problemas - Ex. 61

A água é bombeada de um grande reservatório mais baixo para um reservatório mais alto. Alguém afirma que se a perda de carga for desprezível, a carga de bomba necessária será igual à diferença de elevação entre as superfícies livres dos dois reservatórios. Você concorda?

Passo 1

Temos a seguinte situação:

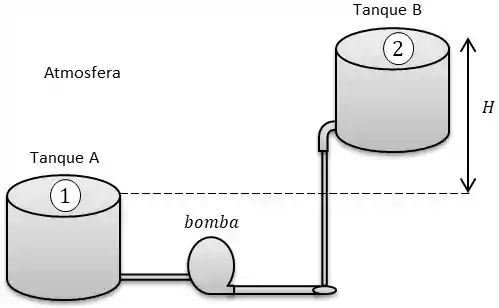
Caso a perda de carga for desprezível, a carga da bomba necessária será igual à diferença de elevação, H , entre as superfícies livres dos tanques.

Vamos executar a equação do balanço energético e verificar isto.

Assumindo que os dois tanques estão abertos para atmosfera. Como os dois pontos estão abertos para atmosfera teremos P 1 = P 2 = P a t m . Tomaremos a superfície livre do tanque A como z 1 = 0   m e superfície livre do tanque B como z 2 = H   m .

Como estamos desprezando todas as perdas de cargas as velocidades de entrada e saída serão as mesmas V 1 = V 2 .

Passo 2

Escrevendo a equação do balanço energético:

P 1 ρ g + α 1 V 1 2 g + z 1 + h b o m b a ,   u t = P 2 ρ g + α 2 V 2 2 2 g + z 2 + h t u r b i n a , e + h L

Simplificaremos P 1 , P 2 , V 1 e V 2 por serem iguais.

z 1 + h b o m b a ,   u t = z 2 + h t u r b i n a , e + h L

Simplificando h t u r b i n a , e (pois, não existe uma) e h L .

z 1 + h b o m b a ,   u t = z 2

Substituindo valores:

0 + h b o m b a ,   u t = H

h b o m b a ,   u t = H

Resposta

Sim, ao desprezarmos todas as perdas de cargas a carga necessária é a diferença entra as superfícies livres de cada tanque.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando a Eq. 2.16, deduza os perfis de velocidade, vazão e velocidade média de um fluido não newtoniano em um tubo circular. Para uma vazão Q = 1μ L / m i n e R = 1m m , com k tendo valor unitário em
Usando a Eq. A.3 no Apêndice A para a viscosidade da água, encontre a viscosidade da água a -20 °C e 120 °C. Trace o gráfico da viscosidade para essa faixa de temperatura. Encontre a vazão laminar máx
Em uma indústria de alimentos, dois fluidos imiscíveis são bombeados através de um tubo de modo que o fluido 1 ( μ 1 = 0,5N . s / m 2 ) forme um núcleo de r = 1 / 4 D 1 e o fluido 2 ( μ 2 = 5N . s / m
Considere escoamento de sangue em uma artéria. O sangue é um fluido não newtoniano; a tensão de cisalhamento versus a taxa de cisalhamento é descrita pela relação de Casson: τ = τ c + μ . d u d r ,p a
Considere escoamento laminar completamente desenvolvido em um tubo circular. Avalie o coeficiente de energia cinética para este escoamento.