Usando a técnica de sublimação do naftaleno, a distribuição radial dos coeficientes de transferência de massa por convecção locais em um escoamento uniforme e normal à superfície de um disco circular foi correlacionada por uma expressão com a forma:

O número de Sherwood no ponto de estagnação depende dos números de Reynolds e de Schmidt , e os dados foram correlacionados pela expressão a seguir:

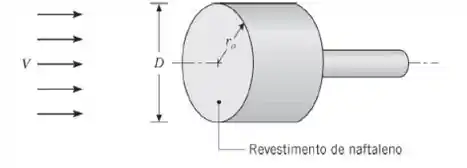
Obtenha uma expressão para o número de Nusselt médio correspondente a transferência de calor em um disco isotérmico exposto ao escoamento descrito anteriormente. Se e , qual é a taxa de transferência de calor saindo de um disco com diâmetro D = 20 mm e temperatura superficial , exposto a uma corrente de ar com ? Tipicamente, o desenvolvimento da camada-limite a partir de um ponto de estagnação fornece um coeficiente convectivo decrescente com o aumento da distância do ponto de estagnação. Dê uma explicação plausível para o motivo do comportamento oposto observado no disco.

E ai galerinha bonitaaa!!

Animados para mais uma??

Sabemos dos exercícios anterior que o número de Nusselt e Sherwood possuem uma certa analogia entre eles:

Assim como:

Como o termo é igual para ambos:

Então:

Para achar nós podemos usar a relação:

Pelo enunciado nós temos:

Substituindo:

Reorganizando nós obtemos:

Substituindo no número de Nusselt:

Substituindo

E com isso nós achamos a expressão para o número de Nusselt!!