Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 70

Para reduzir a ameaça de predadores, o faisão da areia, um pássaro do Quênia, coloca seus ovos em locais distantes de fontes de água. Para trazer água para os seus filhotes, o pássaro voa até a fonte mais próxima e, pela submersão da parte inferior de seu corpo, retém água na sua plumagem. O pássaro, então, retorna para o seu ninho e os filhotes sorvem a água da

plumagem. Obviamente, se o tempo de voo for muito longo, as perdas por evaporação podem causar uma redução significativa da quantidade de água na plumagem e os filhotes podem acabar morrendo por desidratação.

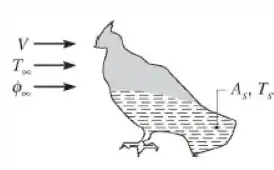
Para adquirir uma melhor compreensão da transferência por convecção durante o voo, estudos em um túnel de vento foram efetuados usando modelos moldados do faisão. Pelo aquecimento da porção do modelo correspondente à da plumagem que armazena a água, um coeficiente de transferência de calor por convecção médio foi determinado. Resultados para diferentes velocidades do ar e tamanhos do modelo foram, então, usados para desenvolver uma correlação empírica com a forma:

N u L - = 0,034 R e L 4 5 P r 1 3

A área da superfície efetiva da porção da plumagem que armazena água é designada por A s e o comprimento característico é definido por L   =   A s 1 2 . Considere condições nas quais um pássaro absorveu 0,05 kg de água na sua plumagem com A s =   0,04   m ² e está retornando ao seu ninho a uma velocidade constante V   =   30 m s . O ar ambiente está em repouso e a uma

temperatura e umidade relativa de T ∞   =   37 ° C e ф ∞ =   25 % , respectivamente. Se durante todo o voo a superfície As estiver coberta por uma película de água líquida a T s   =   32 ° C , qual é a distância máxima permitida entre o ninho e a fonte de água, se o pássaro deve retornar com pelos menos 50% do seu suprimento inicial de água?

Passo 1

Faaaaaaalaa aiii galeraaa !!

Como vocês estão hoje?? Espero que bem animados !!

Neste probleminha beem legal nós queremos a distância máxima que o falcão pode percorrer, não é?

E se lembrarmos lá da física, nós podemos dizer que o deslocamento pode ser calculado em função da velocidade e da variação do tempo:

∆ S = V . ∆ t

O tempo está diretamente relacionado com a vazão mássica, ou seja, a massa evaporada de água pelo tempo:

m ˙ e v a p = ∆ m ∆ t →   ∆ t = ∆ m m ˙ e v a p

Agora nós chegamos em algo que já conhecemos muito bem, a taxa de evaporação da água pode ser escrita como:

m ˙ e v a p = h m - A s ρ A , s - ρ A , ∞

Então nossa equação ficará assim:

∆ S = V . ∆ m h m - A s ρ A , s - ρ A , ∞

Vamos ver o que nós temos?

∆ m = 0,50 × 0,05 k g = 0,025   k g

A s =   0,04   m ²

L   =   A s 1 2 = 0,04   m ² 1 2 = 0,2   m

V   =   30 m s

T ∞   =   37 ° C = 307   K

ф ∞ =   25 %

T s   =   32 ° C + 273 = 305   K

Nós ainda não temos a densidade, certo? Para conseguir acha-las nós vamos usar a Tabela A.6

Para a superfície do pássaro, a 305 K:

ρ A , s = 0,0336 k g m 3

Para o ambiente, a 307 K, nós temos que levar em consideração a umidade:

ρ A , ∞ = 0,25 0,0436 k g m 3

ρ A , ∞ = 0,0 109 k g m 3

Então a única informação que nós ainda não temos é h m - , certo?

Bora encontrar !!

Passo 2

O problema nos disse que:

N u L - = 0,034 R e L 4 5 P r 1 3

De maneira análoga nós podemos concluir que:

S h L - = 0,034 R e L 4 5 S c 1 3

O número de Sherwood é dado por:

S h L - = h m - L D A B

R e L = V L v

S c = v D A B

Substituindo e isolando o coeficiente:

h m - = 0,034 D A B V L v 4 5 v D A B 1 3 L

Sabemos da Tabela A.8 que:

D A B = 0,62 × 10 - 6 m 2 s

E interpolando os dados da Tabela A.4 para achar a velocidade cinemática:

v - 15,89 × 10 - 6 20,92 × 10 - 6 - 15,89 × 10 - 6 = 307 K - 300 K 350   K - 300 K

v = 16,7 × 10 - 6 m 2 s

E agora nós só precisamos substituir:

h m - = 0,034 0,62 × 10 - 6 m 2 s 30 m s 0,2   m 16,7 × 10 - 6 m 2 s 4 5 16,7 × 10 - 6 m 2 s 0,62 × 10 - 6 m 2 s 1 3 0,2   m

h m - = 0,106 m s

Passo 3

Para finalizar nós vamos colocar tudo que achamos na fórmula do Passo 1:

∆ S = 30 m s . 0,025   k g 0,106 m s   0,04   m ² 0,0336 k g m 3 - 0,0109 k g m 3

∆ S = 7785   m

∆ S = 7 , 78   k m

Legal não foi?

Resposta

∆ S = 7,78   k m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na primavera, muitas vezes superfícies de concreto, como calçadas e estradas, ficam muito molhadas no período da manhã, mesmo na ausência de chuva durante a noite. Condições típicas para o período not
Um bem-sucedido engenheiro californiano instalou em seu jardim uma banheira de hidromassagem circular e avaliou que, para as condições de operação típicas descritas no esboço, a água deve ser reposta
Sabe-se que em noites limpas a temperatura do ar não precisa ser inferior a 0°C para que uma fina camada de água sobre o solo se congele. Considere uma dessas camadas de água sobre o solo em uma noite
Uma expressão para a pressão parcial de vapor d’água real em termos das temperaturas de bulbo úmido e de bulbo seco, conhecida por equação de Carrier, é dada por: p v = p s a t ,b u - p - p s a t ,b u
Um refrigerador de névoa é usado para oferecer alívio para um atleta fatigado. Água a T i=10 ° C é injetada como uma névoa em uma corrente de um ventilador a uma temperatura ambiente de T ∞=32 ° C . O