Vapor de água saturado a condensa em um trocador de calor de único casco e 2 tubos com área de superfície de e coeficiente global de transferência de calor de . Água fria que flui a entra no lado do tubo a . Determine a efetividade da transferência de calor, a temperatura de saída da água fria e a taxa de transferência de calor do trocador de calor.
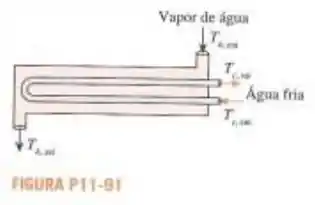
Passo 1
Dados fornecidos:
Temperatura do vapor de água saturada:
Temperatura da água fria:
Vazão mássica da água fria:
Calor especifico da Vapor de água saturado:
Área da superfície de transferência de calor:
Coeficiente global de transferência de calor:
Premissas:
1) Existe uma condição operacional estável.
2) O trocador de calor é bem isolado, de modo que a perda de calor para os arredores é insignificante.
3) As propriedades do fluido são constantes.
4) Alterações nas energias cinética e potencial de fluxos de fluido são desprezíveis.
Passo 2
Fala galera!!!
Para resolver essa questão, temos que calcular as taxas de capacidade térmica dos fluidos quente e frio. Para o fluido quente (vapor de água saturado), temos:
Para o fluido frio (água fria), temos:
Portanto, a menor das duas taxas de capacidade térmica é:
Temos também que a relação das taxas de capacidade é a seguinte:
Passo 3
Fluidos com menor valor de taxa de capacidade experimentam a maior mudança de temperatura, de modo que a taxa máxima de transferência de calor se torna a seguinte:
Substituindo os termos da equação acima pelos dados obtidos, temos:
Passo 4
a) Agora, vamos calcular o para este trocador de calor. Assim temos
Aqui, é o coeficiente global de transferência de calor e é a área da superfície de troca de calor. Substituindo os termos da equação acima pelos dados obtidos, temos:
Neste trocador de calor ocorre uma mudança de faze. Assim, temos que e consequentemente . Pela Tabela 11-4, vemos que a efetividade para trocadores com é dada pela seguinte relação:
Substituindo os termos da equação acima pelos dados obtidos, temos:
Portanto, a efetividade da transferência de calor é .
Passo 5
b) Temos então, que a temperatura de saída da água fria pode ser calculada pela seguinte relação:
Onde é a taxa real de transferência de calor .
Substituindo os termos da equação pelos dados obtidos, temos:
Portanto, a temperatura de saída da água fria é .
Passo 6
c) Temos que a taxa real de transferência de calor pode ser calculada da seguinte maneira:
Portanto, a taxa real de transferência de calor é .
Resposta
a)
b)
c)