Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 55

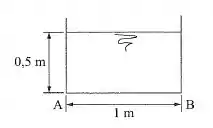
Um veículo move-se com velocidade constante de 100   k m / h para a direita, carregando um recipiente retangular aberto que contém água. O veículo é freado em 10   s até parar com desaceleração constante. Dados: ρ = 1000   k g / m 3 ; g = 10   m / s 2 ; não há transbordamento. Determinar:

  1. A inclinação da superfície livre em relação à horizontal, durante a frenagem;
  2. A pressão nos pontos A e B durante a frenagem.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Durante a frenagem o líquido irá se deslocar formando um prisma trapezoidal como da figura abaixo:

Como a aceleração é constante, temos que:

v = v 0 + a t

Sendo a velocidade final igual a zero e a velocidade inicial do movimento de frenagem igual a 100 k m h = 27,78   m / s , temos que:

a = 27,78 10

a = 2,778   m / s 2

Passo 2

Pela teoria, sabemos que:

a = g tan ⁡ θ

Substituindo os valores, temos que:

tan ⁡ θ = 2,778 10

tan ⁡ θ = 0,2778

Portanto:

θ = tan - 1 ⁡ 0,2778

θ = 15,5 °

Passo 3

O item b, nos pede a pressão nos pontos A e B . A expressão que calcula a diferença de pressão em dois pontos é:

P B - P A = ρ ∆ x a x

Substituindo as variáveis conhecidas, temos que:

P B - P A = 1000 ( 1 ) ( 2,778 )

P B - P A = 2778

Como não houve derramamento de líquido durante a frenagem, temos que a área do líquido no primeiro momento tem que ser igual a área do líquido no segundo momento. Portanto:

h B + h A 2 1 = 0,5 ( 1 )

h B + h A = 1

Multiplicando por γ , temos que:

γ h B + γ h A = γ

P B + P A = 10000

Somando as duas equações, temos que:

2 P B = 12778

P B = 6389   P a

E:

P A = 3611   P a

Resposta

a )   θ = 15,5 °

b )   P A = 3611   P a

P B = 6389   P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suppose that the U-tube of Fig. P2.151 is rotated about axisDC. If the fl uid is water at 1228F and atmospheric pressure is 2116 lbf/ft2 absolute, at what rotation rate will the fluid withinthe tube b
The tank of water in Fig. P2.143 is full and open to the atmosphere at point A. For what acceleration ax in ft/s2 will thepressure at point B be (a) atmospheric and (b) zero absolute?
The 6-ft-radius waterwheel in Fig. P2.149 is being used tolift water with its 1-ft-diameter half-cylinder blades. If thewheel rotates at 10 r/min and rigid-body motion is assumed,what is the water sur
Figure P2.160 shows a gage for very low pressures, invented in 1874 by Herbert McLeod. (a) Can you deduce,from the fi gure, how it works? (b) If not, read about it andexplain it to the class.
Figure P2.161 shows a sketch of a commercial pressuregage. (a) Can you deduce, from the fi gure, how it works?