Um viscosímetro de cilindros concêntricos é mostrado. O torque viscoso é produzido pela folga anular em torno do cilindro interno. Um torque viscoso adicional é produzido pelo fundo plano do cilindro interno à medida que gira acima do fundo plano do cilindro externo estacionário. Obtenha expressões algébricas para o torque viscoso devido ao escoamento na folga anular de largura a e para o torque viscoso devido ao escoamento na folga do fundo de altura b. Faça um gráfico mostrando a razão, b/a, necessária para manter o torque do fundo a 1%, ou menos, do torque do espaço anular, versus as outras variáveis geométricas. Quais são as implicações do projeto? Que modificações no projeto você recomendaria?
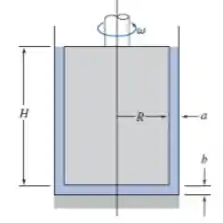
Passo 1
Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Assumindo que o líquido em questão é newtoniano e que a velocidade é de perfil linear, temos que:
O torque gerado por uma superfície anular é dado por:
Já o torque no fundo é:
Pegando o caso do problema, temos que:
Substituindo e isolando :
Fazendo o gráfico:
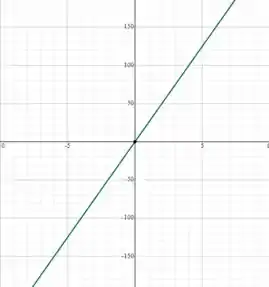
Para algum específico, a dimensão pode ser efetivamente aumentada escavando-se o cilindro, como mostrado no gráfico acima.
Resposta
Para algum específico, a dimensão pode ser efetivamente aumentada escavando-se o cilindro, como mostrado no gráfico acima.