Indução Eletrostática
Produzido por Bruno SoaresTeoria
Fala aí, seja muito bem vindo ao Responde Aí! Bora conversar sobre Indução Eletrostática?
📢 Clique para saber mais:
O que é Indução Eletrostática?
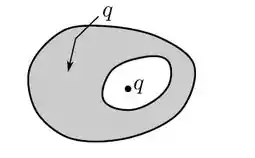
Através da Indução eletrostática a gente consegue carregar eletricamente um objeto sem que haja contato. Para isso a gente só precisa colocar nosso objeto dentro do campo elétrico de um objeto carregado!
-Mas como eu coloco um objeto dentro do campo elétrico de outro?! 😖
É muito simples, você só precisa aproxima-los! Assim:
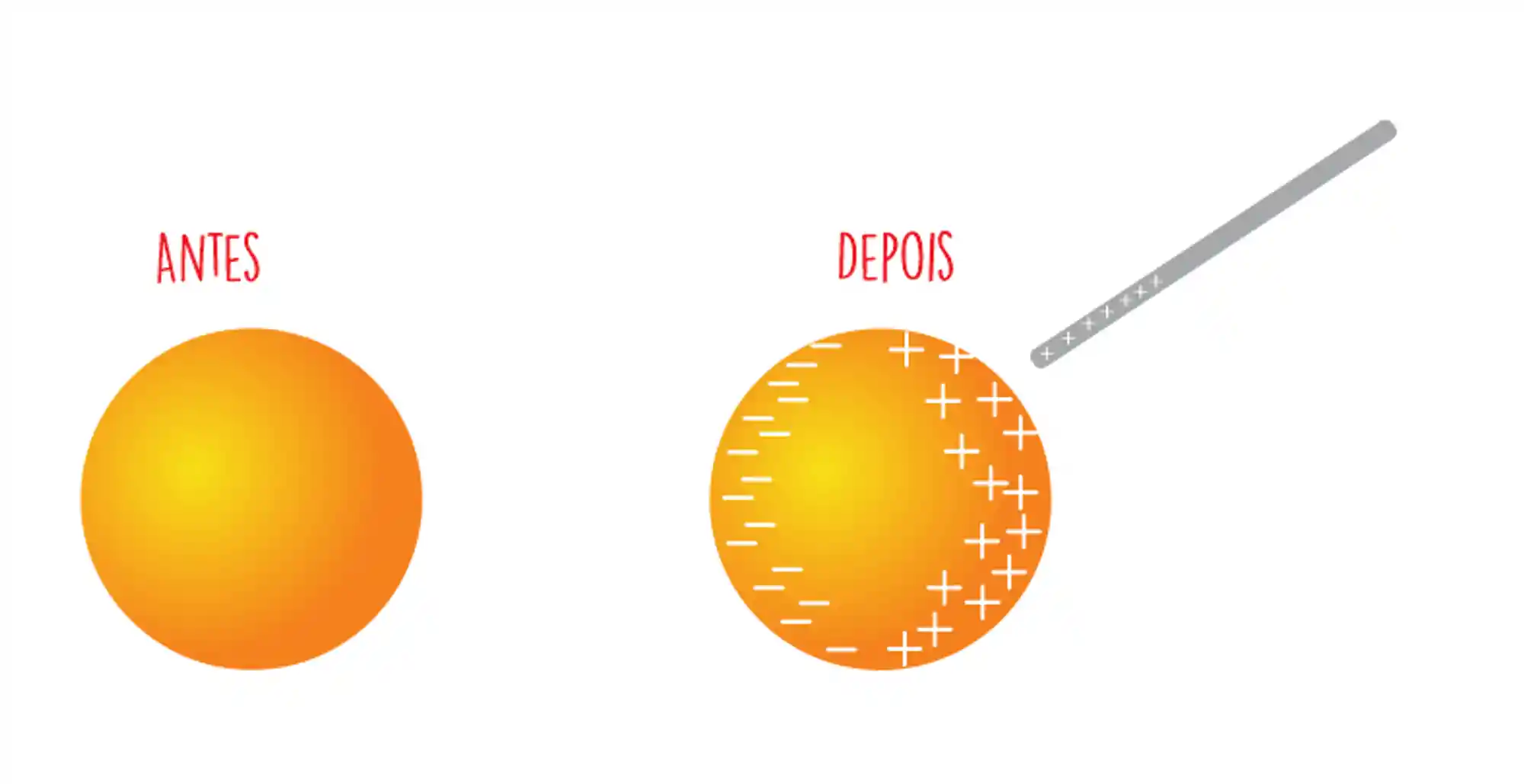
Nesse exemplo acima, aproximamos uma barra de candutora, de metal, carregada positivamente de uma esfera de metal eletricamente neutra. Vamos entender direitinho o que acontece depois na esfera:
- As cargas de sinal oposto às da barra (cargas negativas) vão querer se aproximar dela;
- As cargas de mesmo sinal que as da barra (cargas positivas) vão querer ir para mais longe possível dela.
Esse fenômeno que ocorre na esfera é a eletrização por indução! 🤩
-Beleza, mas como isso pode ser cobrado em exercícios?!
Pra saber isso e muito mais, se liga nesse vídeo completaço que o Responde Aí preparou pra você! 😍 👇
Problemas com Cascas Esféricas
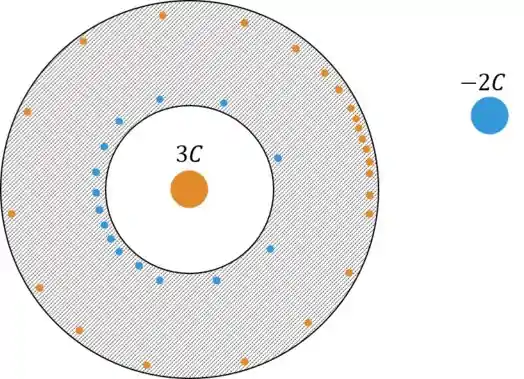
Agora, vamos analisar aqui as questões que envolvem cascas esféricas! Para isso vamos fazer um exemplo, considere a seguinte casca esférica neutra:
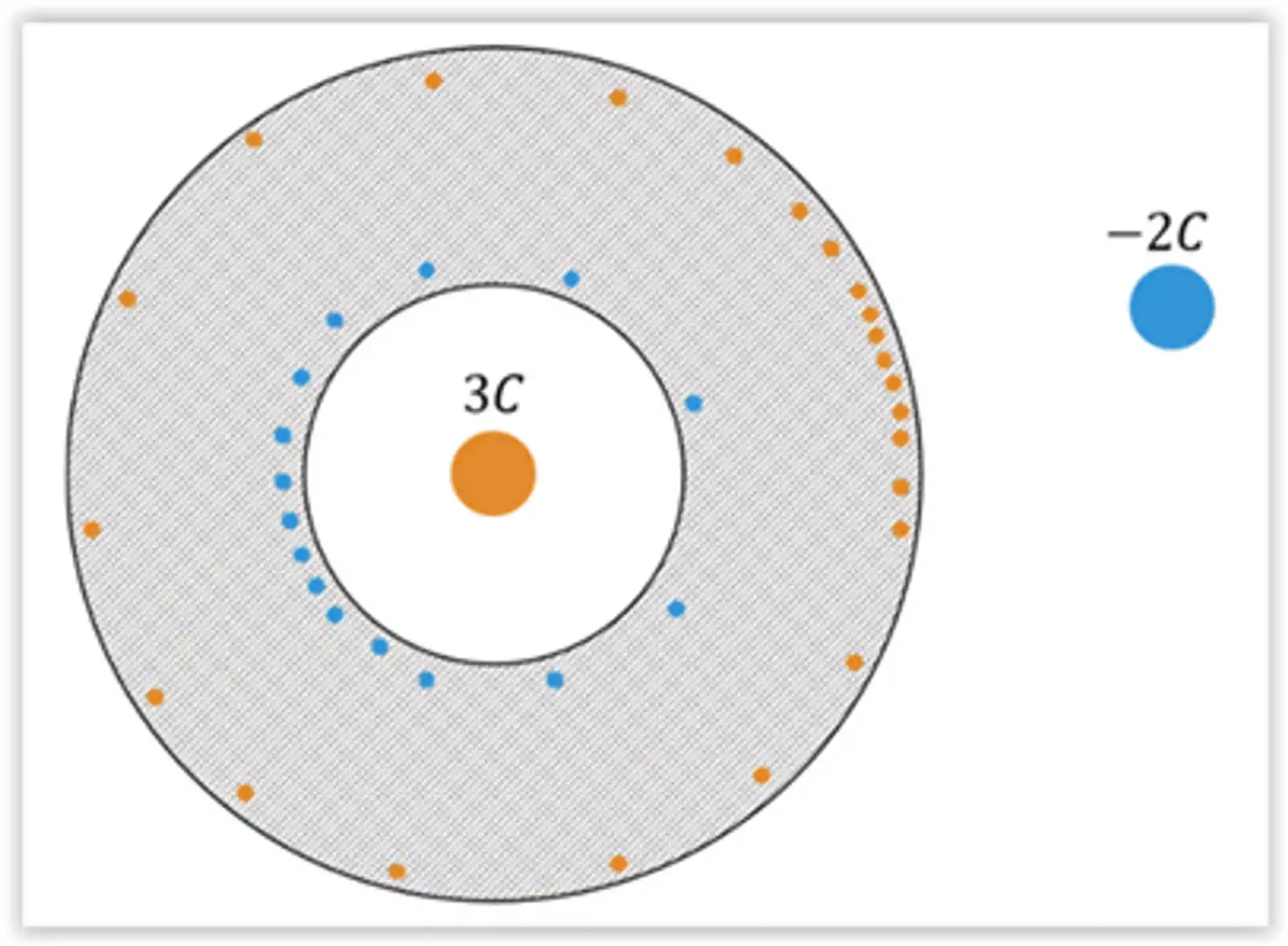
No interior da casca esférica, temos uma carga positiva de 3C , que vai trazer as cargas negativas da casca para próximo da superfície interna, por indução. Já no exterior da casca esférica, temos uma carga de -2C , que vai “puxar” as cargas positivas para a superfície externa da casca.
Um exercício pode pedir pra você dizer o quanto de carga fica induzido por dentro e o quanto de carga fica induzido por fora da casca. Para isso o raciocínio, neste caso, é o seguinte:
- No interior da casca, a carga positiva induz uma carga de mesmo módulo e sinal oposto na superfície interna, ou seja, de -3C.
- No exterior, sobra uma carga de +3C, já que a casca esférica é neutra.
A forma como as cargas se distribuem na superfície externa é alterada pela presença da carga negativa de -2C. Assim a casca começa e termina neutra! A carga interna foi quem determinou o quanto de carga fica induzido na parte de dentro e a carga de fora não influencia nas contas, apenas muda a distribuição delas na parte de fora da casca.
Agora vamos supor que a casca esférica já começa carregada! Nesse caso, devemos proceder de forma muito parecida, considerando o seguinte:
- O corpo de dentro induz na superfície interior da casca uma carga de mesmo módulo e sinal oposto (e isso independe da carga inicial da casca).
- A carga que sobra se distribui pelo resto da casca esférica.
- A carga que está na parte exterior da casca só serve para alterar a distribuição das cargas, sem mudar a carga total no exterior e no interior.
A ideia é a mesma quando consideramos múltiplas cascas, uma dentro da outra. Agora vamos praticar com exercícios?!
Problemas com Cascas Esféricas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Dada uma esfera condutora de carga total zero, aproxima-se uma carga puntiforme positiva dela. Assinale a opção correta:
- Nada ocorre pois a esfera é neutra.
- A esfera é atraída, por conta das cargas negativas que são induzidas na proximidade da carga puntiforme positiva.
- A esfera é repelida, por conta das cargas positivas que são induzidas na proximidade da carga puntiforme positiva.
- A esfera vai pedir um Uber para ir à Esferolândia
Passo 1
Vamos analisar a situação com um desenho esquemático.
Quando se aproxima uma carga positiva de um corpo neutro, o que ocorre é uma indução de cargas, ou seja, as cargas negativas que o compõe são atraídas para a superfície mais próxima da carga puntiforme positiva.
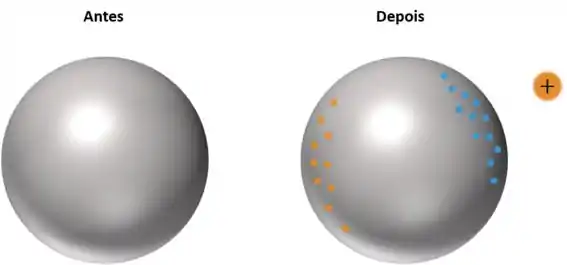
Passo 2
Agora podemos observar que as cargas negativas estão mais próximas da carga positiva. Como cargas de sinais opostos se atraem, isto significa que a esfera será atraída pela carga positiva, e vice versa.
Resposta
Letra b.
Exercício Resolvido #2
Elaboração Própria
Uma esfera condutora maciça tem um buraco esférico em seu interior, no qual é colocada (não me pergunte como) uma carga puntiforme de .
Dado que a esfera maciça é neutra, calcule a quantidade de cargas em cada uma das superfícies dela (interna e externa) após a inserção da carga e atingido o equilíbrio eletrostático.
Passo 1
Este é um problema de indução com conservação de cargas. Como não há contato entre os corpos, a carga total na esfera antes é igual à carga total nela após colocada a carga no buraco. Portanto:
Sabemos que a esfera é neutra, portanto:
Por consequência a carga no final deve ser zero também.
Passo 2
Como é inserida na parte oca uma carga puntiforme de , esta mesma carga vai induzir na superfície interna uma carga de . Portanto:
Descobrimos quanto de carga existe na superfície interna!
Como no equilíbrio eletrostático as cargas só podem se encontrar nas superfícies, temos:
E sabemos, pelo passo , que a carga total no condutor deve ser zero sempre, logo:
Fim de papo!
Resposta
Exercício Resolvido #3
Elaboração Própria
Uma esfera condutora maciça tem um buraco esférico em seu interior, no qual é colocada (utilizando-se magia) uma carga puntiforme de . Ao lado da esfera é colocada uma carga puntiforme de , conforme o desenho:
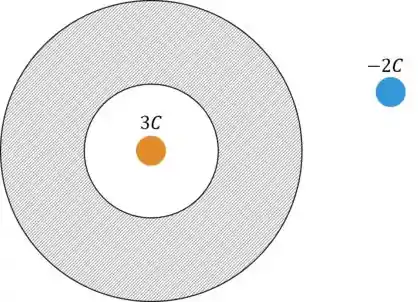
Dado que a esfera maciça tinha carga total de , calcule a quantidade de cargas em cada uma das superfícies dela (interna e externa) após atingido o equilíbrio eletrostático.
Passo 1
Por indução, na superfície interna vamos ter uma carga de , que é atraída pela puntiforme de no interior da parte oca:
Passo 2
Bom, por conservação de cargas, temos que a carga total no condutor é sempre :
Além disso, ao atingir o equilíbrio eletrostático, só haverá cargas nas superfícies, portanto:
Logo, substituímos os valores:
Note que a carga de no exterior não influi em nada. O único efeito que ela vai ter é de concentrar cargas na parte da superfície que está mais próxima dela, mas o total de cargas lá seria o mesmo, caso esta carga não existisse.
Resposta
Exercício Resolvido #4
UFF-Física II-Lista de Exercícios2-Exercício n°2
Uma pequena esfera de metal está pendurada por uma linha isolante dentro de uma esfera condutora grande e oca, como na figura. Um fio condutor estendido atravessa a pequena esfera e o pequeno orifício na esfera oca, porém sem tocá-la. Um bastão carregado é usado para transferir carga positiva para o segmento do fio que está fora da esfera oca. Após o bastão carregado ter tocado o fio e ter sido removido as seguintes superfícies estarão com carga positiva, carga negativa ou descarregada? Explique.
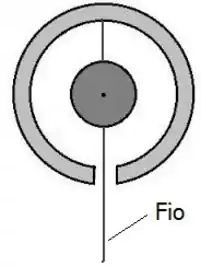
A pequena esfera.
A superfície interna da oca.
A superfície externa da esfera oca.
Passo 1
Depois de o bastão carregado transferir cargas positivas (ou melhor dizendo, receber cargas negativas do fio condutor, já que são as cargas negativas que podem se mover!) para o fio condutor, temos que as cargas se distribuirão pela pequena esfera de metal, de modo a obter a configuração de menor energia possível. Além disso, temos que as cargas estarão distribuídas na superfície da esfera, por se tratar de um condutor.
Logo, teremos que a pequena esfera está positivamente carregada.
Passo 2
Por termos a pequena esfera de metal positivamente carregada, serão induzidas, na superfície interna da esfera oca, cargas negativas e de mesmo módulo que a carga da pequena esfera.
Logo, será induzida, na superfície interna da esfera oca, uma carga negativa de mesmo módulo que carga que está presente na pequena esfera pendurada.
Passo 3
Pensando apenas na esfera oca, como ela estava neutra anteriormente, e não recebeu nenhum tipo de carga, temos que ela permanece neutra, ou seja, o número de cargas positivas é igual ao de cargas negativas. Como foi induzida uma carga negativa na superfície interna, e lembrando que não temos campo no interior de um condutor, uma carga positiva será induzida na superfície externa da esfera oca, e está terá o mesmo módulo que a carga negativa induzida na superfície interna.
Será induzida, na superfície externa da esfera oca, uma carga positiva de mesmo módulo que a carga negativa induzida na superfície interna da esfera oca.
Resposta
A pequena esfera está positivamente carregada.
Será induzida, na superfície interna da esfera oca, uma carga negativa de mesmo módulo que carga que está presente na pequena esfera pendurada.
Será induzida, na superfície externa da esfera oca, uma carga positiva de mesmo módulo que a carga negativa induzida na superfície interna da esfera oca.
Exercício Resolvido #5
Young & Freedman, Física III Eletromagnetismo, 14ª ed. Pearson, Cap. 21, pp. 32
Você tem um objeto com carga negativa. Como pode usá-lo para colocar carga negativa em uma esfera metálica isolada e neutra? E para colocar carga positiva na esfera?
Passo 1
Esse problema está dividido em duas partes: a primeira delas é colocar uma carga negativa na esfera metálica. Bem, para isso precisamos apenas enconstar o objeto carregado na esfera e, como os dois materiais são condutores, uma parte dessas cargas negativas vai passar para a esfera, até que os dois objetos entrem em equilíbrio eletrostático.
Passo 2
Já na segunda parte do problema, queremos colocar uma carga positiva na esfera. Agora, vamos apenas aproximar o objeto carregado da esfera. O que vai acontecer é: cargas positivas na esfera vão se aproximar das cargas negativas do objeto e as cargas negativas na esfera vão se afastar do objeto, como na figura abaixo.
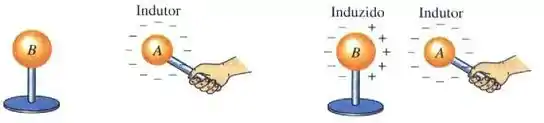
Mas e agora, como podemos “sumir” com as cargas negativas da esfera? Bem, para isso, podemos conectar a o lado esquerdo da esfera com a Terra por um fio condutor, mantendo sempre o nosso objeto carregado próximo do lado direito da esfera. Como a Terra é condutora e bem maior que a nossa esfera, uma parte dos elétrons vai passar pelo fio em direção à Terra.
Aí, desconectamos o fio condutor e afastamos o objeto carregado e pronto! Nossa esfera fica carregada positivamente ;)
Resposta
Colocar carga negativa: enconstar o objeto carregado na esfera.
Colocar carga positiva: aproximar o objeto carregado, aterrar a esfera e, por fim, desconectar o fio e afastar o objeto.
Exercício Resolvido #6
Elaboração própria.
Aproxima-se uma partícula puntiforme carregada positivamente de uma esfera condutora, neutra e isolada. Após restabelecido o equilíbrio eletrostático, responda:
a) Como é a distribuição de cargas na esfera condutora? A força entre a esfera e carga é nula, atrativa ou repulsiva? Explique.
b) A esfera é aterrada e, depois de o aterramento ser desfeito, qual é a carga que essa esfera possuirá?
c) Após o aterramento ser desfeito, a força entre a esfera e a carga pontual será nula, atrativa ou repulsiva?
Passo 1
a) A presença dessa carga induz uma redistribuição das cargas positiva e negativa da esfera condutora neutra, cuja carga total é . Uma carga negativa se redistribui mais sobre a superfície direita da esfera, se aproximando de e outra carga se afasta de se distribuindo mais sobre a superfície à esquerda da esfera condutora, como mostra a figura.
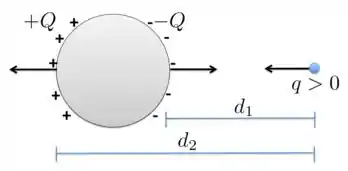
Como , a intensidade da força de aproximação entre e é maior do que a de afastamento entre e . Por isso, ainda que a esfera seja neutra, ou seja, carga total , a presença de uma carga resultará em um força atrativa resultante sobre a esfera que é diferente de zero.
Passo 2
b) Quando a esfera é aterrada, a Terra, que é um grande condutor, neutraliza as cargas positivas da esfera que estão mais afastadas da carga . Por isso, depois desse aterramento, a esfera possuirá carga negativa que tenderá a se distribuir uniformemente sobre a superfície da esfera.
Passo 3
c) Como a carga sobre a superfície da esfera será negativa, então continuará havendo atração entre ela e a carga pontual .
Resposta
- O campo elétrico dentro da esfera é nulo e a força entre a esfera condutora e a carga puntiforme será de atração ;
- Após o aterramento, a carga sobre a esfera condutora será negativa;
- A força entre a esfera e carga pontual será de atração.
Exercício Resolvido #7
Elaboração própria.
Considere a seguinte sequência de eventos:
- Duas esferas metálicas, iguais e neutras, são colocadas em contato;
- Um bastão com carga positiva é aproximado dessas esferas em contato, vindo mais próximo de uma delas, mas sem tocá-las;
- As esferas são separadas por uma pequena distância uma da outra, mas ainda com o bastão carregado positivamente próximo delas;
- O bastão positivo agora é afastado e, em seguida, as esferas ficam bastante afastadas entre si;
Após essa sequência de eventos, como é a distribuição de cargas sobre cada uma das esferas condutoras?
Passo 1
Condutores neutros em contato tornam-se carregados com cargas opostas quando um bastão positivo se aproxima, pois ele atrai os elétrons para extremidade esquerda da esfera mais próxima dele, deixando a esfera da direita com a carga positiva, como a gente mostra na Figura abaixo.

Quando as esferas são separadas por uma pequena distância, mas ainda com o bastão positivo por perto, elas continuam com suas cargas iguais e de sinais opostos, como a gente na próxima Figura.

Depois que o bastão é removido para bem longe das esferas e elas são afastadas de maneira que carga de uma não afeta a carga da outra, a distribuição de cargas sobre a superfície de cada esfera tende a ficar uniforme, e uma esfera fica com carga positiva e a outra com carga negativa, como está Figura abaixo.

Resposta
No final do processo, uma das esferas possui carga negativa e a outra fica com carga positiva, e as cargas tendem a ficar distribuídas uniformemente sobre a superfície das esferas condutoras.
Exercício Resolvido #8
Elaboração própria.
Considere a seguinte sequência de eventos:
- Um bastão carregado positivamente é aproximado de uma esfera neutra condutora;
- Ainda como o bastão positivo por perto, a esfera condutora é aterrada;
- O aterramento da esfera é desfeito, sem que se retire o bastão positivo;
- O bastão positivo agora é afastado para bem longe da esfera;
Após essa sequência de eventos, como é a distribuição de cargas sobre a esfera condutora?
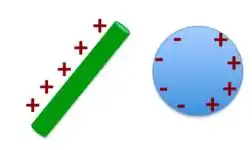
Passo 1
Quando o bastão positivo se aproxima da esfera, a carga livre nessa esfera condutora fica polarizada e suas cargas negativas vão para a sua extremidade esquerda se aproximando do bastão, como está Figura abaixo.
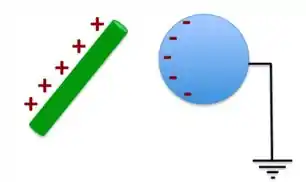
Quando essa esfera condutora é aterrada, como está na próxima Figura, a Terra, que é um grande condutor fornecedor de partículas carregadas, neutraliza as cargas positivas que estão distantes do bastão à direita da esfera metálica.
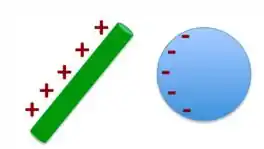
Depois disso, se o aterramento é desfeito, mas com o bastão ainda por perto, a esfera condutora tem carga negativa, mas ainda espalhada e polarizada sobre a extremidade mais à esquerda de sua superfície.
Agora, se o bastão é removido para bem longe da esfera, a distribuição de cargas dessa esfera será negativa e tenderá a ficar espalhada de maneira uniforme sobre sua superfície, como está Figura abaixo.

Resposta
No final do processo, a esfera metálica fica com carga negativa distribuída uniformemente sobre sua superfície.
Exercício Resolvido #9
Paul A. Tipler, Gene Mosca, Física para cientistas e engenheiros, Volume 2, 6˚ ed., Editora LTC, Problema 40, pp. 67.
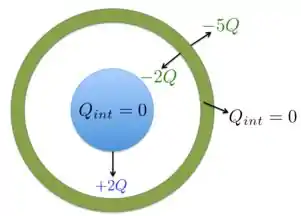
Considere a esfera sólida condutora e a casca esférica condutora concêntrica mostrada na Figura abaixo. A casca esférica tem carga . A esfera sólida tem carga .
- Quanta carga está na superfície interna da casca esférica?
- Considere, agora, que um fio metálico seja conectado entre a esfera sólida e a casca. Depois de o equilíbrio eletrostático ser restabelecido, quanta carga está na esfera sólida e em cada superfície da casca esférica?

Passo 1
a) Como a casca esférica externa é condutora, o campo elétrico dela, no equilíbrio eletrostático, é zero. Ou seja, no interior da região verde da Figura, o campo elétrico é zero e qualquer excesso de carga nessa casca vai para a superfície dela.
O mesmo acontece com a esfera sólida que está dentro da cascas. A carga dela está uniformemente distribuída sobre sua superfície e não tem campo elétrico dentro dessa esfera sólida.
Bom, como a carga líquida de todo o sistema é , então, uma carga de vai ficar na superfície interna da casca esférica, como está na Figura abaixo. O restante da carga total da casca esférica, que é , vai para a sua superfície externa.
Passo 2
b) Agora, dá uma olhada na Figura acima. Se a gente conectar um fio condutor entre a superfície da esfera condutora sólida e superfície interna da casca condutora, haverá um cancelamento das cargas e após o equilíbrio eletrostático ser restabelecido e restará apenas a carga sobre a superfície externa da casca esférica.
Nessa situação, não haverá campo elétrico entre as esferas, já que haverá cancelamento das cargas por causa do fio condutor.
Resposta
- Na região no interior da casca esférica não haverá carga e estará sobre a superfície externa da casca esférica.
Exercício Resolvido #10
UFRJ, Física 3, P1 – 2013.1, Questão ME01
Um condutor com uma cavidade encontra-se em equilíbrio eletrostático e possui uma carga total . No interior da cavidade, existe uma partícula em repouso, de carga também . Quais são as cargas nas superfícies interna e externa do condutor, respectivamente?
(a) e .
(b) e .
(c) e .
(d) e .
(e) e .
Passo 1
Primeiramente vamos analisar a carga no interior da cavidade.
A carga da partícula é . Ela vai atrair cargas de sinal contrário presentes no condutor. Portanto, uma carga total igual a irá se distribuir na superfície interna do condutor.
Podemos ver que a questão já foi resolvida pois a única opção possível agora é a letra (a), mas vamos continuar =)
Passo 2
Como a carga total do condutor é de e nós temos na superfície interna, precisamos compensar essa carga positiva com para que a carga total no condutor seja .
Lembrando que em um condutor as cargas irão se posicionar na superfície externa. A não ser que o condutor possua uma cavidade e que haja uma carga posicionada dentro desta cavidade.
Passo 3
Portanto temos que:
Como eu havia dito, a resposta é a letra (a) =)
Resposta
(a) e .
Exercício Resolvido #11
UFRJ, Física 3, P1 – 2011.2, Questão ME04
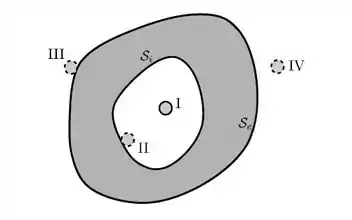
Temos um condutor oco, com carga Q, em equilíbrio eletrostático, conforme mostra a figura.
Com uma pequena esfera condutora, também de carga Q, considere as quatro seguintes situações:
(I) a esfera é colocada dentro da cavidade oca, sem tocar a superfície interna. (II) a esfera é colocada dentro da cavidade, em contato com a superfície interna . (III) a esfera é colocada em contato com a superfície externa do condutor oco. (IV) a esfera é colocada na vizinhança (externa) do condutor oco, sem tocar nele.
Após atingido o equilíbrio eletrostático e referindo-se às cargas nas superfície interna e
externa do condutor oco como e , respectivamente, qual das alternativas corresponde
às quatro situações descritas anteriormente?
(a) I: ; II: ; III: ; IV:
(b) I: ; II: ; III: ;IV:
(c) I: ; II: ; III: ; IV:
(d) I: ; II: ; III: ; IV:
(e) I: ; II: ; III: ; IV:
Passo 1
Bom, vamos por partes e analisar o que vai acontecer em cada caso para as cargas da superfície interna e externa.
Lembrando que condutores só possuem cargas nas superfícies e por isso analisaremos apenas a superfície interna e externa e não a parte oca em si.
Após isso vamos comparar com as respostas e ver qual delas está coerente com o que constatarmos.
Passo 2
Começaremos pelo item (I) quando a esfera é colocada na parte oca sem tocar a superfície interna :
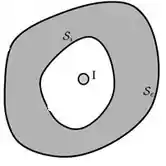
Se a pequena esfera no interior da cavidade tem carga Q, ela irá atrair cargas de sinal oposto para a superfície interna do condutor. Portanto .
Mas se o condutor esta carregado com uma carga Q, precisamos compensar essa carga da superfície interna com uma carga 2Q na superfície externa:
Entao...
Passo 3
Pro item (II) a esfera é colocada dentro da cavidade, em contato com a superfície interna .
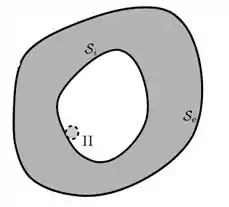
Se a pequena esfera é colocada dentro da cavidade e em contato com o condutor, toda a carga da pequena esfera irá para o condutor e ficará na superfície externa deste. Lembra? Em um condutor em equilíbrio eletrostático as cargas se distribuem na superfície (externa).
Pensa da seguinte maneira, as cargas de mesmo sinal tendem a se repelir certo? Entao elas vao se colocar na posição em q cada uma esteja o mais afastada da outra, ou seja, na superfície. Entendeu? =)
Então...
Passo 4
No item (III): a esfera é colocada em contato com a superfície externa do condutor oco.
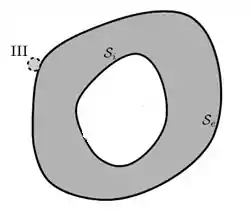
Esse ítem é um pouquinho mais complicado, vamos precisar usar uma formula que aparece quando dois condutores de tamanhos diferentes são unidos.
Assim como no ítem anterior, não haverá carga na superfície interna do condutor.
Com relação a carga na superfície externa precisamos avaliar:
Lembra daquela formula da teoria ?
Vamos aplicar ele no problema:
Como o enunciado diz que a esfera é pequena, podemos supor que e rearranjando a equação acima temos:
E portanto
Ou seja, tem muito mais carga no condutor que na esfera pequena e podemos considerar que toda carga estará na superfície externa do condutor.
Então...
Passo 5
No ítem (IV): a esfera é colocada na vizinhança (externa) do condutor oco, sem tocar nele.
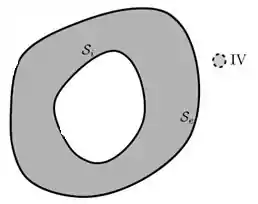
Assim como nos dois ítens anteriores, não haverá carga na superfície interna do condutor.
Com relação a carga na superfície externa, podemos perceber que a carga do condutor continuará a ser Q e a da pequena esfera também continuará a ser Q. A única coisa que irá ocorrer é que as cargas das duas vão se repelir, se localizando com maior densidade na extremidade oposta à que está mais próxima uma da outra.
Então:
Podemos verificar que a resposta é a letra (c)
Resposta
(c) I:
II:
III:
IV: