Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 10.Exercícios e Problemas - Ex. 29

| A é o diagrama de energia potencial para uma partícula de que é liberada do repouso em .

A partícula se moverá para a direita ou para a esquerda? Como você pode descobrir?

Qual é velocidade máxima da partícula? Em que posição ela possui tal velocidade?

Onde se encontram os pontos de retorno do movimento?

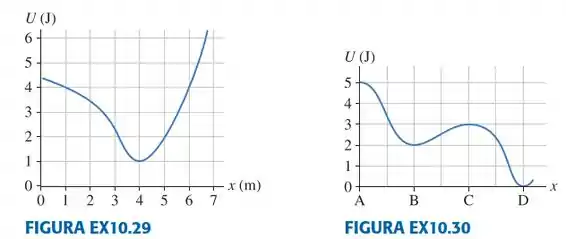
Passo 1

A partícula se moverá para a direita ou para a esquerda? Como você pode descobrir?

Nesse tipo de deslocamento a energia total se mantém em todos os pontos, mas ela pode ser decomposta em Energia Cinética () e Energia potencial (), de modo que :

Partindo da liberação da partícula (Não há movimento, ), traçamos uma linha para esse valor será fixo, e vale, pelo gráfico , observe:

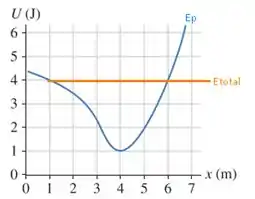
Veja que para segundo o gráfico , esse é um detalhe que as vezes passa despercebido, veja:

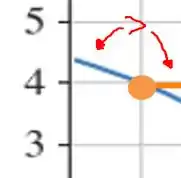
Matematicamente:

Por tanto, deve ser negativo para manter. Só que a energia cinética negativa é anti-física! Então a partícula não pode se mover para a esquerda de . Ou seja, a partícula se moverá para a direita de obrigatoriamente.

Passo 2

Qual é velocidade máxima da partícula? Em que posição ela possui tal velocidade?

A velocidade (sempre associada a ) vai ser máxima na parte mais funda da curva, por que é quando a vai ser mínima segundo o gráfico, e o corpo vai precisar da máxima para manter o ! Lembre:

Esse ponto vai ser em :

Passo 3

Onde se encontram os pontos de retorno do movimento?

È quando volta a ter seu valor de origem quando foi liberado, então serão:

Resposta

Para a direita de

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13. mola de uma arma de brinquedo atira uma bola de plástico com rapidez v 0 . A mola, então, é comprimida em uma distância duas vezes maior do que na primeira vez em que foi disparada. Por que fator

12. Uma mola está comprimida em 10c m . Em quanto deve ser comprimida uma mola de constante elástica duas vezes maior a fim de armazenar a mesma quantidade de energia?

11. Ordene, em sequência decrescente, as quantidades de energia potencial elástica de U e a a U e d armazenadas nas molas da FIGURA Q10.11. Explique.

14. Uma partícula com a energia potencial mostrada na FIGURA Q10.14 move-se para a direita do ponto x = 5m com energia total E . a . Em que valores de x a velocidade da partícula atinge um máximo? b .

Os elásticos de um estilingue se alongam mediante uma tensão segundo a lei ∆ L = 5,0 c m N T é a tensão em cada elástico. Uma criança alonga seu estilingue de um valor ∆ L = 25c m para atirar uma pedr