Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 10.Questões Conceituais - Ex. 11

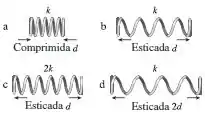
11. Ordene, em sequência decrescente, as quantidades de energia potencial elástica de U e a a U e d armazenadas nas molas da FIGURA Q10.11. Explique.

Passo 1

Vem comigo! Juntos vamos resolver esse problema.

A chave para ordenar as energias potenciais na forma que o enunciado pede vai ser usarmos a seguinte equação da energia potencial elástica.

U e = 1 2 k ' Δ x 2

Como você pode ver, os parâmetros k e Δ x são os cruciais para o valor de U e , então vamos avaliar cada mola da figura com as informações que ela nos dá.

Uma outra observação é que como Δ x está elevado ao quadrado então o fato da mola está comprimindo o esticando não altera o sinal da energia, o que vai interessar mesmo é o módulo de Δ x .

Passo 2

Vamos começar então com a mola ( a ) , temos o seguinte para esse caso.

k ' = k

Δ x = d

Logo temos a seguinte energia potencial elástica.

U e a = 1 2 k d 2

Passo 3

Agora vamos analisar a mola ( b ) , para essa mola temos:

k ' = k

Δ x = d

Logo temos a seguinte energia potencial elástica.

U e b = 1 2 k d 2

Passo 4

Agora vamos analisar a mola ( c ) , para essa mola temos:

k ' = 2 k

Δ x = d

Logo temos a seguinte energia potencial elástica.

U e c = 1 2 2 k d 2

⇒ U e c = k d 2

Passo 5

Por último para a mola ( d ) temos:

k ' = k

Δ x = 2 d

Logo temos a seguinte energia potencial elástica.

U e d = 1 2 k 4 d 2

⇒ U e d = 2 k d 2

Passo 6

Agora o que falta é colocar as energias que encontramos em ordem decrescente.

Olhando nossas energias vemos que a maior energia que temos é U e d , depois temos a U e c e por último temos as menores energias que são iguais U e a e U e b , assim temos:

U e d > U e c > U e a = U e b

Resposta

U e d > U e c > U e a = U e b

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma atiradeira lança verticalmente um seixo de 10g até um altura de 22,0m . a) Qual é a energia potencial elástica armazenada nas tiras de borracha da atiradeira? b) Qual seria a altura atingida por u
Uma mola ideal de massa desprezível tem 12,0 cm de comprimento quando nada está preso a ela. Ao pendurarmos um peso de 3,15 kg nessa mola, seu comprimento passa a ser 13,40 cm.Para que armazene 10,0 J
Uma mola armazena energia potencial U 0 quando está comprimida em uma distância x 0 em relação ao seu comprimento sem deformação. (a) Em termos de U 0 , quanta energia ela rmazena quando está comprimi
Considere o cavaleiro do Exemplo 7.7 (Seção 7.2) e a Figura 7.16. Como no exemplo, o cavaleiro é libertado a partir do repouso quando a mola está esticada 0,100 m. Qual é o deslocamento x do cavaleiro
Um queijo de 1,20k g é colocado sobre uma mola de massa desprezível e constante k = 1800N / m que está comprimida 15,0c m . Até que altura acima da posição inicial o queijo se eleva, quando a mola é l