Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 10.Questões Conceituais - Ex. 14
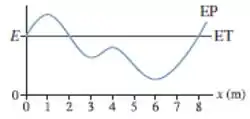
14. Uma partícula com a energia potencial mostrada na FIGURA Q10.14 move-se para a direita do ponto com energia total .
Em que valores de a velocidade da partícula atinge um máximo?
Essa partícula possui algum ponto ou pontos de retorno na faixa de valores de coberta pelo gráfico? Em caso afirmativo, onde?
Se for alterada adequadamente, a partícula poderia permanecer em repouso em algum ponto ou pontos da faixa de valores de coberta pelo gráfico? Em caso afirmativo, onde?
Passo 1
Então meu consagradx, para esse problema temos que ter em mente uma coisa principalmente, que:
E com isso na análise do gráfico temos que a diferença entre a linha de energia total com o gráfico da energia potencial temos a energia cinética.
Uma coisa que temos que ter em mente é que não podemos ter uma energia potencial maior que a energia total, logo a partícula só pode estar confinada na parte em que
Passo 2
Vamos então começar a responder o item .
Para a partícula ter a maior velocidade ela precisa ter a maior energia cinética.
Como falamos no passo temos que:
Como o valor de é constante temos que ver o ponto no gráfico onde temos o menor valor de , pois assim temos a maior energia cinética.
Olhando o gráfico vemos que isso acontece em .
Passo 3
O item quer os valores de onde temos pontos de retorno.
Esses pontos acontecem quando estamos nos limites dos gráficos, onde temos , já que não podemos ter . Graficamente esses pontos se encontram nas interseções da reta da energia total e do gráfico de energia potencial.
No nosso gráfico temos que isso acontece em e em .
Passo 4
Agora vamos para o item .
Para que esse repouso ocorra teríamos que ter uma energia total igual a máximos ou mínimos da energia potencial. Então isso pode ocorrer na situação do enunciado já que a energia potencial apresenta máximos e mínimos.
Isso iria ocorrer conforme mexemos na energia total em , em e em .