Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 8.Problemas Adicionais - Ex. 134
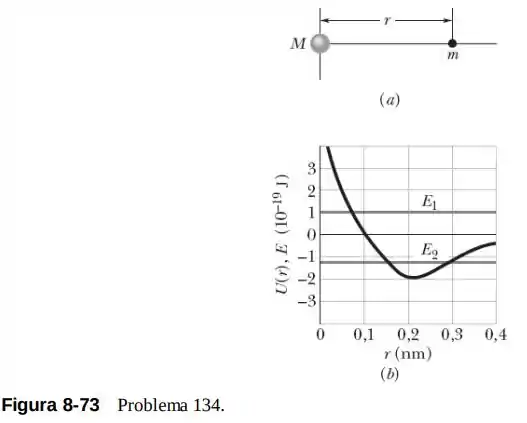
134- A Fig. 8-73a mostra uma molécula composta por dois átomos de massas e (com ) separados por uma distância . A Fig. 8-73b mostra a energia potencial da molécula em função de .
Descreva o movimento dos átomos (a) se a energia mecânica total do sistema de dois átomos for maior que zero (como ) e
(b) se for menor que zero (como ). Para e ,
determine (c) a energia potencial do sistema,
(d) a energia cinética total dos átomos e
(e) a força (módulo e orientação) que atua sobre cada átomo. Para que valores de a força é (f) repulsiva, (g) atrativa e (h) nula?
Passo 1
Imagina um sistema massa mola onde temos a presença de apenas duas energias, a elástica e a cinética. Quando a mola atinge sua energia máxima, logo temos que a energia elástica da mola se iguala a energia mecânica, mas logo em seguida ela volta pois a mola e a cinética passam a puxar ela de volta. A mesma coisa acontece com esses átomos, pelo menos fica fácil ver para a pois se a massa estiver numa região que parece ser entre a massa oscilará indefinidamente nessa região. Já para energia mecânica igual a podemos dizer que se a massa encontra-se em um o átomo tenderá a ir para esse ponto e depois voltará .
Passo 2
c) Para no gráfico temos
d) Logo como a energia mecânica é de logo:
Então a cinética será:
Passo 3
e) A força pela teoria é dada por:
Para a região de temos uma variação positiva, logo a força seria negativa. O valor é difícil precisar mais considerando essa região uma reta podemos dizer que ela varia de a cada então por alto podemos dizer que a força é de:
e) A força é repulsiva em regiões onde a energia potencial é decrescente (forças positivas em relação ao eixo horizontal, isso é da esquerda para a direita) , logo de:
f) A força é atrativa em regiões onde a energia potencial é decrescente (forças negativas em relação ao eixo horizontal com origem na massa ):
g) Por fim a força é nula onde a energia potencial tem ponto de máximo ou de mínimo, que será em: