Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 8.Problemas Adicionais - Ex. 126

126- Para fazer um pêndulo, uma bola de 300 g é presa a uma das extremidades de uma corda com 1,4 m de comprimento e massa desprezível. (A outra extremidade da corda está fixa.) A bola é puxada para um lado até a corda fazer um ângulo de 30,0° com a vertical; em seguida (com a corda esticada) a bola é liberada a partir do repouso.

Determine (a) a velocidade da bola quando a corda faz um ângulo de 20,0° com a vertical

e (b) a velocidade máxima da bola.

(c) Qual é o ângulo entre a corda e a vertical quando a velocidade da bola é igual a um terço do valor máximo?

Passo 1

Fazendo o desenho do pêndulo temos:

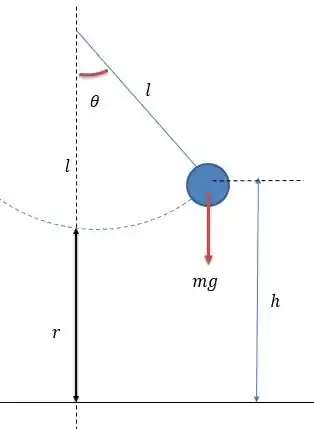
Vamos considerar que inicialmente o pêndulo está no ângulo de 30 a energia cinética desse ponto é de 0 e a altura do pêndulo pelo desenho é de:

h = r + l - l c o s   θ = r + l ( 1 - cos ⁡ 30 )

Logo a energia mecânica em θ = 30   será de:

E 0 = 0 + m g ( r + l ( 1 - cos ⁡ 30 )

Agora para um θ um pouco menor igual a θ 1 teremos uma energia cinética associada e uma altura diferenciada o que nos dará:

E d = 1 2 m v 2 + m g ( r + l ( 1 - cos ⁡ θ 1 )

Como não há atritos vamos igualar as duas:

m g ( r + l ( 1 - cos ⁡ 30 ) = 1 2 m v 2 + m g ( r + l ( 1 - cos ⁡ θ 1 )

Isolando a velocidade v temos:

1 2 m v 2 = m g ( r + l 1 - cos ⁡ 30 ) - r - l ( 1 - cos ⁡ θ 1 )

1 2 m v 2 = m g l ( cos ⁡ θ 1 - cos ⁡ 30 )

v = 2 g l ( cos ⁡ θ 1 - cos ⁡ 30 )

Para θ = 20 temos:

v = 2 × 9.81 × 1.4 ( cos ⁡ 20 - cos ⁡ 30 ) = 1.42   m / s

Passo 2

Derivando a equação da velocidade que encontramos em relação a θ e igualando a zero encontramos:

d v d θ 1 = - 2 g l s i n   θ 1 2 2 g l ( cos ⁡ θ 1 - cos ⁡ 30 )   = 0

O valor que satisfaz esse valor e é menor que zero é θ 1 = 0 . Logo nesse valor de θ teremos nossa velocidade máxima.

Logo ela será:

v = 2 × 9.81 × 1.4 ( cos ⁡ 0 - cos ⁡ 30 ) = 1.92   m / s

Passo 3

Um terço do valor máximo nos dá:

v = 1.92 3 = 0.64   m / s

Substituindo temos:

0.64 = 2 × 9.81 × 1.4 ( cos ⁡ θ 1 - cos ⁡ 30 )

Resolvendo:

0.4096 = 27.468 ( cos ⁡ θ 1 - cos ⁡ 30 )

0.015 = cos ⁡ θ 1 - cos ⁡ 30

0.881 = cos ⁡ θ 1

θ 1 = cos - 1 ⁡ 0.881 = 28.24 °  

Resposta

a )   1.42   m / s

b )   1.92   m / s

c )   28.24 °  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Tarzan, que pesa 688N , salta de um penhasco pendurado na extremidade de um cipó com 18m de comprimento (Fig. 8-38). Do alto do penhasco até o ponto mais baixo da trajetória, ele desce 3,2m . O cipó s
Um praticante de rapel desce uma face de um penhasco quando tropeça e começa a deslizar sobre a rocha, preso apenas à corda de b u n g e e - j u m p que está presa no topo do penhasco. A face do penha
A bolinha de um pêndulo de comprimento L é puxada lateralmente até que o fio forme um ângulo θ 0 com a vertical e então seja liberada. No exemplo 7-5, a conservação da energia foi usada para obter a r
Um pêndulo é afastado da vertical de um ângulo de 60 ° e solto em repouso. Para que ângulo com a vertical sua velocidade será metade da velocidade máxima atingida pelo pêndulo?