Exercícios de Energia Cinética + Energia Gravitacional + Energia Elástica - Lista de Exercícios Resolvida
Questão 1
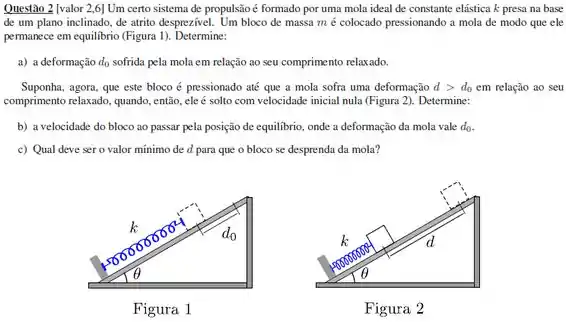
Um pêndulo está suspenso do teto e preso a uma mola que, por sua vez, está presa ao chão em um ponto diretamente abaixo do suporte do pêndulo. A massa da bolinha do pêndulo é , o comprimento do pêndulo é e a constante da força é . O comprimento da mola frouxa é e a distância entre o chão e o teto é . O pêndulo é puxado lateralmente, de modo a formar um ângulo com a vertical e é então liberado do repouso. Obtenha uma expressão para a rapidez da bolinha, quando ela passa pelo ponto diretamente abaixo do suporte do pêndulo.

Questão 2
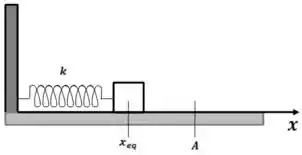
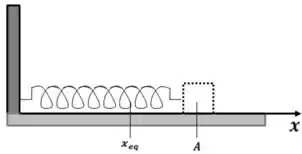
Um pequeno bloco de massa está sobre uma superfície horizontal sem atrito ligado a uma mola de constande elástica cuja outra extremidade é fixa em uma parede, como mostra a figura. O bloco é deslocado para , a partir da posição de equilíbrio, e liberado a partir do repouso. Para qualquer instante posterior, o módulo da sua velocicade é dado por:
Questão 3
O objeto de é largado do repouso de uma altura de em uma rampa curva sem atrito. Na base da rampa está uma mola com constante de força de . O objeto desliza rampa abaixo e até a mola, comprimindo-a de uma distância até atingir momentaneamente o repouso.
- Encontre .
- Descreva o movimento do objeto (se ocorrer) após o repouso momentâneo.

Questão 4
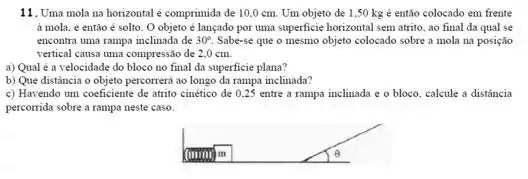
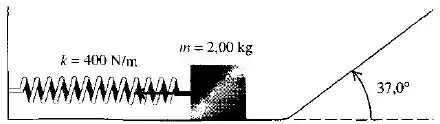
Um bloco de é empurrado contra uma mola de massa desprezível e constante , comprimindo a mola até uma distancia igual a . Quando o bloco é libertado, ele se move ao longo de uma superfície horizontal sem atrito e sobre um plano inclinado de . a) Qual a velocidade do bloco enquanto ele desliza ao longo da superfície horizontal depois de abandonar a mola? b) Qual a distancia máxima que ele atinge ao subir o plano inclinado até parar antes de voltar para a base do plano?
Questão 5
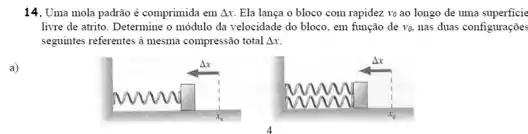
Um anel de peso está preso a uma mola e desliza sem atrito num fio circular situado num plano vertical, conforme a figura.
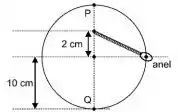
Considerando que a mola não se deforma quando o anel se encontra na posição e que a velocidade do anel seja a mesma nas posições e , a constante elástica da mola deve ser de:
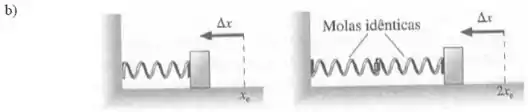
Questão 6
Dois blocos estão ligados por um fio leve que passa por uma roldana de massa desprezível e sem atrito. O bloco de massa está sobre uma superfície lisa sem atrito, preso a uma mola de constante elástica , que por sua vez se prende ao bloco de massa . O sistema é solto, a partir do repouso, com a mola sem qualquer deformação.
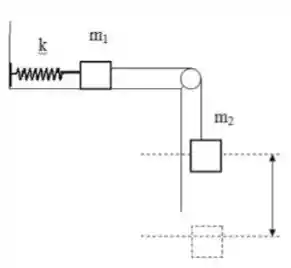
a) Faça na figura acima um diagrama das forças atuando nos blocos em algum momento após o sistema ser solto.
b) Através do teorema de trabalho-energia, calcule quanto o sistema se desloca até ficar momentaneamente em repouso novamente.
c) Calcule a velocidade do bloco 2 quando este se deslocou a partir do ponto inicial, quando os blocos estão em repouso.
Ver solução completaQuestão 7
Um bloco encontra-se em equilíbrio suspenso por uma mola de constante elástica , presa ao teto com alongamento . O bloco é levantado até a posição em que o alongamento é nulo e abandonado a partir do respouso. Ao descer uma altura o bloco ganha uma energia cinética,
Questão 8
Um bloco de massa está localizado no final de uma mola de constante elástica comprimida de . Após um certo instante, esta mola é solta e dispara o bloco, fazendo com que ele adquira velocidade e suba uma pequena rampa de altura . Ao final desta rampa, o bloco encontra um piso cujo o coeficiente de atrito entre o bloco e o piso vale . Todas as superfícies antes de atingir o piso do final da rampa possuem coeficiente de atrito desprezível. Dado: use para a gravidade.

b) Em função de , , e determine a velocidade do bloco no final da rampa antes de atingir o trecho com atrito.
Ver solução completaQuestão 9
Um bloco de massa está localizado no final de uma mola de constante elástica comprimida de . Após um certo instante, esta mola é solta e dispara o bloco, fazendo com que ele adquira velocidade e suba uma pequena rampa de altura . Ao final desta rampa, o bloco encontra um piso cujo o coeficiente de atrito entre o bloco e o piso vale . Todas as superfícies antes de atingir o piso do final da rampa possuem coeficiente de atrito desprezível. Dado: use para a gravidade.

a) Em função de , e determine a velocidade adquirida do bloco logo após se soltar da mola.
Ver solução completaQuestão 10
Um bloco de massa está preso por um fio a uma mola de constante elástica . O fio passa por uma polia de cujo momento de inércia em relação ao seu eixo de rotação é . O fio tem massa desprezível, é inextensível e não desliza sobre a polia, que pode girar sem atrito em torno do seu eixo de rotação. O bloco é liberado em repouso e com a mola relaxada. Qual é a rapidez do bloco depois de ter caído ?
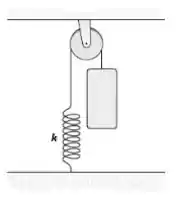
(A)(B)(C)(D)(E)
Ver solução completaQuestão 11
Um objeto de massa , que parte do repouso, desliza sobre um plano inclinado e posteriormente percorre uma pista circular vertical de raio , conforme ilustrado na figura abaixo. Durante todo o movimento, o atrito sobre o objeto é desprezível. Qual o menor valor possível para (ver figura abaixo) para que o objeto percorra a trajetória circular sem nunca perder contato com a pista?
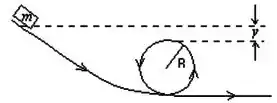
(A)
(B)
(C)
(D)
(E) zero
Ver solução completaQuestão 12
Um objeto é largado de uma altura . Se a resistência do ar puder ser desprezada, qual dos gráficos abaixo descreve corretamente a energia mecânica deste objeto como função de sua altura, ?
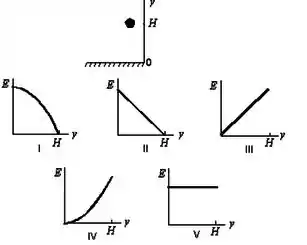
(A) I
(B) II
(C) III
(D) IV
(E) V
Ver solução completaQuestão 13
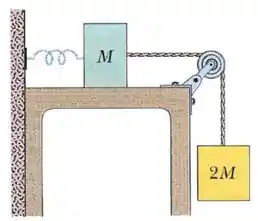
Dois blocos de massas e estão presos a uma mola de constante elástica que tem uma das extremidades fixa, como mostra a figura. Não há atrito entre o bloco e a superfície horizontal nem no eixo da polia, cuja massa é desprezível. Os blocos são liberados a partir do repouso com a mola relaxada. Qual é a energia cinética do bloco que está pendurado depois de ter descido ?
(A) 0,45 J
(B) 0,90 J
(C) 1,8 J
(D) 2,7 J
(E) 3,6 J
Ver solução completaQuestão 15
(Capítulo 8.5 – Exercício 31) Na Fig. 8-40, um bloco de massa é liberado a partir do repouso em um plano inclinado sem atrito de ângulo . Abaixo do bloco há uma mola que pode ser comprimida por uma força de . O bloco para momentaneamente após comprimir a mola . (a) Que distância o bloco desce ao longo do plano da posição de repouso inicial até o ponto em que para momentaneamente? (b) Qual é a velocidade do bloco no momento em que entra em contato com a mola?
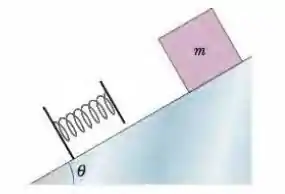
Figura 8-40 Problema 29
Ver solução completaQuestão 16
Uma pessoa de massa salta de uma plataforma amarrada pelos pés a um elástico de tamanho e constante elástica , preso à plataforma. Calcule qual o tamanho máximo atingido pelo elástico.
Questão 17
3 – Num parque de diversão, um trenó de massa parte do repouso e desliza sobre um tobogã de altura inicial , com um loop de raio . Depois de descer o loop, o carrinho ainda tem de trilho até tocar em uma mola de contenção que freia o trenó, com que pode ser comprimida, no máximo, . Para suavizar a colisão, os engenheiros modificaram a superfície ao longo da distância após o loop para que houvesse uma força de atrito para ajudar a frear o carro.

a) qual a altura inicial necessária para que o carrinho complete o loop?
b) considere o coeficiente de atrito entre o trenó e a superfície horizontal depois do loop como sendo e a altura . A constante elástica da mola é grande o suficiente para fazer o carro parar? Justifique com cálculos e explique.
Ver solução completaQuestão 18
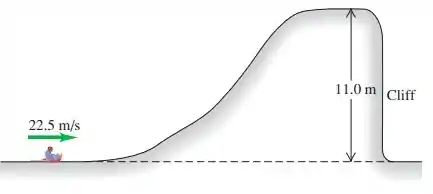
Um trenó com um passageiro tem massa total (trenó + passageiro) de e percorre uma colina congelada perfeitamente lisa como mostrada na figura abaixo. Em que ponto o trenó “aterrissará”, em relação a base do penhasco (cliff)?
Questão 20
Uma partícula de massa é arremessada verticalmente com velocidade inicial para cima. Quando a altura dela é da altura máxima atingida, o módulo de sua velocidade será
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 21
Uma bola de ping-pong pesa 2,5 x N. A bola é colocada dentro de uma taça fixada a uma mola vertical. Quando a mola está comprimida de 5,5 x m, a bola é solta. A altura máxima que a bola atinge, a partir da posição de compressão da mola, é igual a 2,8 m. Desprezando a resistência do ar, determine a constante elástica da mola.

(A) 46 N/m
(B) 24 N/m
(C) 92 N/m
(D) 52 N/m
(E) 56 N/m
Ver solução completaQuestão 22
(Cap 7 – Ex 34) Uma máquina de Atwood, consiste em duas massas, e , e uma polia sem massa e sem atrito. Partindo do repouso, a rapidez das duas massas chega a ao final de . Nesse tempo, a energia cinética do sistemas atinge e cada massa terá se deslocado uma distância de . Determine os valores de e .

Questão 23
Dois blocos estão ligados por um fio leve que passa por uma roldana de massa desprezível e sem atrito. O bloco de massa está sobre uma superfície lisa sem atrito, preso a uma mola de constante elástica , que por sua vez se prende ao bloco de massa . O sistema é solto, a partir do repouso, com a mola sem qualquer deformação.
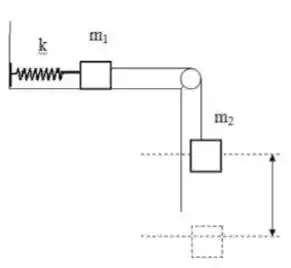
a) Faça na figura acima um diagrama das forças atuando nos blocos em algum momento após o sistema ser solto.
b) Através do teorema de trabalho-energia, calcule quanto o sistema se desloca até ficar momentaneamente em repouso novamente.
c) Calcule a velocidade do bloco 2 quando este se deslocou a partir do ponto inicial, quando os blocos estão em repouso.
Ver solução completaQuestão 24
Um bloco é abandonado do repouso e cai sobre uma mola ideal. Considere o movimento entre o instante em que o bloco é abandonado e aquele em que a mola atinge seu ponto de compressão máxima, antes de o bloco ser arremessado de volta para cima. Sobre as variações das energias cinética , potencial gravitacional e potencial elástica da mola é correto afirmar que:
Questão 25
Considere o gráfico da energia potencial associada à única força que atua sobre a partícula, em função da posição no movimento unidimensional de uma partícula de massa .
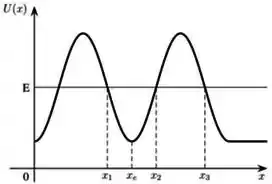
Considere também que a partícula possui energia mecânica indicada no gráfico. Qual a única correta das afirmativas abaixo:
- Por ser um ponto de equilíbiro, a velocidade da partícula nesse ponto é nula.
- Se em um dado instante a partícula estiver em uma posição , ela nunca atingirá a posição .
- Se a partícula está na posição , a força sobre ela será nula.
- Se a partícula está na posição , a força sobre ela aponta no sentido positivo do eixo .
- Se em um dado instante a partícula estiver em uma posição , ela nunca atingirá a posição .
Questão 26
Um bloco de massa inicialmente em repouso desliza para baixo em um plano inclinado que faz um ângulo com a horizontal. Depois de ter deslizado uma distância , o bloco colide com uma mola de constante elástica desconhecida. A mola reduz a velocidade do bloco até fazê-lo parar momentaneamente. Neste instante a mola está comprimida de uma distância . Não existe atrito entre o plano e o bloco até o contato com a mola (deslocamento ). Mas existe atrito entre plano e o bloco na região da mola (deslocamento ) com coeficiente de atrito cinético . Use para a aceleração da gravidade. Responda em função dos dados fornecidos utilizando a Lei de Conservação de Energia.
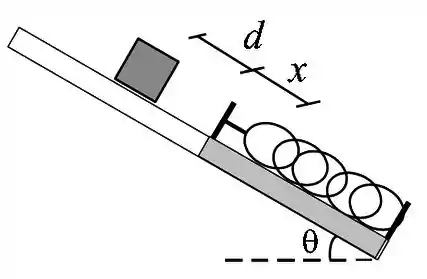
(a) Determine a energia cinética que o bloco possui na iminência de colidir com a mola, em função das variáveis.
Ver solução completaQuestão 27
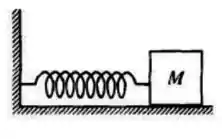
Uma mola ideal sem massa tem uma de suas extremidades fixada à parede, como mostra a Figura. Umbloco de massa é ligado à outra extremidade da mola e está livre para oscilar com uma amplitude sobre uma superfície horizontal sem atrito. A velocidade máxima do bloco é A constante de força da mola é:
Questão 28
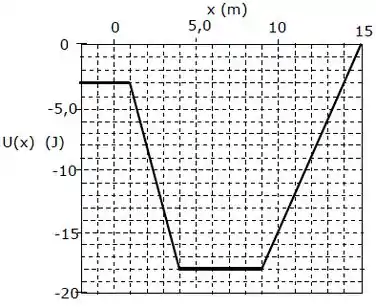
O gráfico abaixo mostra a energia potencial em joules associada à força conservativa que age sobre um corpo de massa . Quando o corpo está em sua velocidade é . Quando o corpo passa pela posição é correto afirmar que sua energia cinética é:
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 29
Um bloco está em movimento sobre um trilho horizontal sem atrito quando encontra o trilho circular vertical, também sem atrito, mostrado na figura. O bloco passa pelos pontos antes de retornar ao trilho horizontal. No ponto :
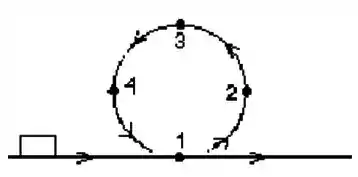
(a) a energia mecânica do bloco é máxima
(b) a força resultante sobre o bloco é zero
(c) a aceleração do bloco é zero
(d) a rapidez do bloco é mínima
(e) a força resultante sobre o bloco aponta para cima
Ver solução completaQuestão 30
Uma bola de a uma velocidade de atinge uma mola de constante elástica igual a que sofre uma compressão de . Calcule a constante elástica da mola. (Considere )
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 31
A energia potencial de uma partícula de 0,20 kg movendo-se ao longo do eixo x é dada por , onde x é expresso em m e U(x) em J. Quando a partícula está em x = 1,0 m ela está viajando na direção x positiva e com rapidez de 5,0 m/s. Em seguida ela irá parar momentaneamente para inverter seu movimento. Qual é está posição x ?
a) -2,3m
b) 2,3m
c) -1,1m
d) 1,1m
e) 0
Ver solução completaQuestão 32
Um bloco de massa é pendurado em uma mola, fazendo com que o seu ponto de equilíbrio se desloque centímetros, como mostrado na Figura. O bloco de é então substituído por um bloco de , e o novo bloco é solto partir da posição representada, na qual a mola não está esticada nem comprimida (ponto de equilíbrio). Até aonde o bloco de vai cair antes que se inverta o sentido do movimento?
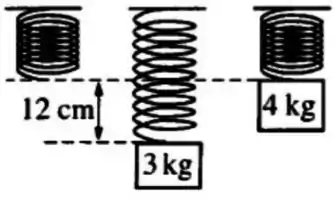
a)
b)
c)
d)
e)
Ver solução completaQuestão 34
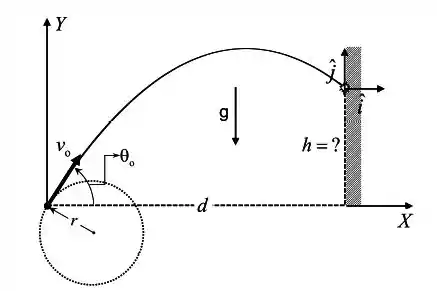
Uma pedra de massa e amarrada a um barbante de comprimento é posta para girar em um plano perpendicular ao solo. Em um dado instante ela é solta de forma que, após passar por uma altura máxima, ela vem a atingir uma parede que se encontra a uma distância do ponto de lançamento. A velocidade da pedra no momento do lançamento tem módulo e faz um ângulo com a horizontal. Nestas condições, determine (Todas as respostas devem ser dadas em termos de , , , , e ):
(a) A altura do ponto de impacto da pedra na parede em relação ao ponto de lançamento
(b) a expressão para o vetor velocidade da pedra no momento imediatamente antes dela atingir a parede, em termos dos vetores unitários e indicados na figura
(c) A energia cinética da pedra no instante em que ela passa pelo ponto mais alto de sua trajetória
(d) o módulo da tensão no barbante no momento imediatamente anterior ao lançamento
Questão 35
Uma balança é formada por um prato de massa desprezível pendurado em uma mola ideal que se distende de quando um corpo de massa é pesado nesta balança. Uma bola de de massa fresca de pão, guardada numa prateleira acima do prato da balança, escorrega da prateleira e cai sobre ele.
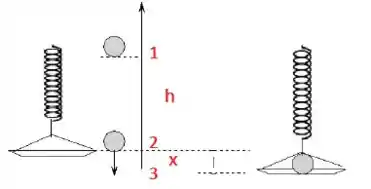
Calcule a constante elástica da mola.
Calcule a energia cinética da bola de massa fresca de pão ao atingir o prato da balança.
Qual a distensão máxima na mola após o prato da balança ser atingido pela bola?
Ver solução completaQuestão 36
Um bloco de se move com uma velocidade de sobre uma superfície horizontal sem atrito, dirigindo-se contra uma mola cuja constante elástica é dada por e que possui uma de suas extremidades presa a uma parede (ver figura abaixo).
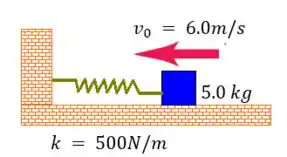
a) Calcule a distância máxima que a mola pode ser comprimida.
Ver solução completaQuestão 37
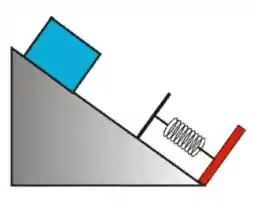
Um bloco de massa é solto, a partir do repouso, em um plano inclinado de em relação à horizontal, com coeficiente de atrito cinético . Depois de percorrer uma distância de ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava inicialmente relaxada, de acordo com o esquema mostrado na figura ao lado.
b) Qual a energia dissipada pelo atrito durante o trajeto do bloco desde o alto do plano até a compressão total da mola? Essa energia dissipada corresponde a que fração da variação total de energia potencial durante o trajeto?
Questão 38
Uma pessoa mantém um bloco de massa em repouso preso a uma mola ideal de constante elástica , comprimida de uma distância medida a partir de sua posição de equilíbrio (figura à esquerda). A massa é solta, sobe e decola da mola, atingindo a altura (definida a partir da posição inicial da massa) com a velocidade (figura direita).
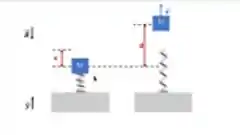
Considere e calcule .
Escolha uma:
Nenhuma das outras alternativas está correta.
Ver solução completaQuestão 41
[ENUNCIADO COMUM ÀS QUESTÕES 3 E 4]
Um bloco de massa é colocado sobre uma mola, de massa desprezível e constante elástica , que possui a outra extremidade fixa em uma superfície horizontal. Na figura (A), a mola está comprimida de em relação a sua posição não deformada. A figura (B) mostra o sistema depois de ter sido liberado, com o bloco atingindo uma altura máxima em relação à sua posição inicial [na figura (A)]. Considere
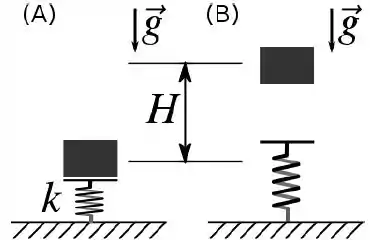
[QUESTÕES 4]
Suponha agora que . Qual é a altura máxima atingida pelo bloco?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 42
Um conhecido brinquedo consiste em uma pista contendo um “loop” circular de raio e um trecho horizontal . No ponto , localiza-se um lançador, constituído de uma mola ideal relaxada, de constante elástica . Um carrinho (representado por um pequeno bloco na figura abaixo) de massa é colocado inicialmente em . Empurra-se o carrinho, comprimindo-se a mola de até o ponto . Neste ponto o carrinho é liberado a partir do repouso perfazendo o percurso , perdendo contanto com a mola no ponto e percorrendo todo o “loop” sem perder contato com a sua superfície. Desprezando-se o atrito em todo o percurso e considerando como dados do problema:
, , , e , calcule:
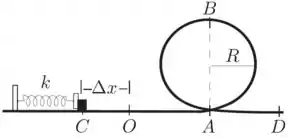
- O módulo da velocidade do carrinho ao passar por ;
- O módulo da velocidade do carrinho ao passar por ;
- Represente em um diagrama as forças que atuam sobre o carrinho ao passar por e determine o módulo da força de contato, , neste ponto;
- A compressão mínima da mola para que, ao passar por , o carrinho esteja na iminência de perder o contato com o “loop”.
Questão 43
Uma mola de constante elástica tem uma de suas extremidades fixas em um ponto e um corpo de massa preso à outra extremidade. A mola tem comprimento de repouso , massa desprezível e pode girar sem atrito em torno do ponto . Em um dado instante [figura (I)] o sistema massa-mola se encontra na posição horizontal com a mola indeformada, sendo, então, liberado a partir do repouso. Ao passar pela posição mostrada na figura (II) sabe-se que a distância do corpo de massa ao ponto é igual a . A aceleração gravitacional no local tem módulo . Assinale a alternativa correta quanto ao módulo da velocidade do corpo na posição da figura (II).
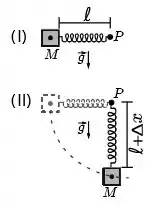
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 44
Um bloco de massa está se movendo inicalmente para direita, sobre uma superfície horizontal sem atrito, com velocidade . Ele então comprime uma mola de constante elástica . No instante em que a energia cinética do bloco é igual à energia potencial da mola, a compressão da mola é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 45
Um sistema formado por dois blocos de mesma massa , presos por uma mola de constante elástica e massa desprezível, encontra-se incialmente em repouso, apoiado sobre o chão conforme a situação () da figura abaixo.
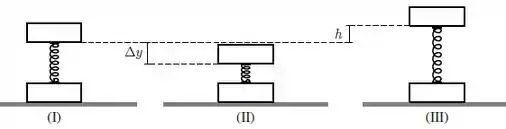
a) Em relação a seu comprimento natural, de quanto a mola está comprimida quando o sistema se encontra em equilíbrio [na situação ()]? A resposta deve ser dada em termos de , e .
b) Faça um diagrama das forças que atuam em cada um dos blocos na situação do item anterior.
c) Um agente externo empurra o bloco de cima, fazendo com que este abaixe de uma distância adicional em relação a posição de equilíbrio, conforme mostrado na situação (). Em seguida, o bloco de cima é liberado. Qual a altura máxima , em relação à posição de equilíbrio, atingida pelo bloco de cima, supondo que o bloco de baixo não perde contato com o solo [situação () da figura]? A resposta deve ser dada em termos de , , e .
d) Qual o valor máximo de para que o bloco de baixo nunca perca contato com o chão? A resposta deve ser dada em termos de , e .
Ver solução completaQuestão 46
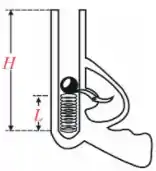
Q - Um revólver de brinquedo é usado para disparar projéteis de massa , verticalmente, utilizando para isso a compressão de uma mola de constante elástica e comprimento natural (não deformada) . Quando o revólver é preparado para atirar, a mola é comprimida e seu comprimento é . Desprezando
atritos e resistência com o ar, e sabendo que o comprimento interno do cano é , a
velocidade do projétil, em , quando sai do cano após o disparo é:
• Considere o projétil como uma partícula de massa .
Questão 48
Uma criança desce o escorrega de um parque de diversões com velocidade de módulo constante. A transformação de energia envolvida é
(A)
(B)
(C)
(D)
(E) Não existe transformação alguma pois a energia do sistema é conservada
Ver solução completaQuestão 49
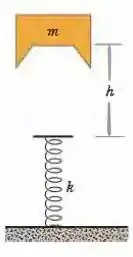
(Capítulo 8.5 – Exercício 22) Um bloco de massa é deixado cair de uma altura sobre uma mola de constante elástica . Determine a variação máxima de comprimento da mola ao ser comprimida.
Questão 50
(Capítulo 8.5 – Exercício 27) A Fig. 8-34 mostra uma pedra de em repouso sobre uma mola. A mola é comprimida pela pedra. (a) Qual é a constante elástica da mola? (b) A pedra é empurrada mais para baixo e liberada. Qual é a energia potencial elástica da mola comprimida antes de ser liberada? (c) Qual é a variação da energia potencial gravitacional do sistema pedra-Terra quando a pedra se desloca do ponto onde foi liberada até a altura máxima? (d) Qual é essa altura máxima, medida a partir do ponto onde a pedra foi liberada?

Questão 51
(Capítulo 8.5 – Exercício 18) Um bloco de é liberado a partir do repouso de uma altura acima de uma mola vertical com constante elástica e massa desprezível. O bloco se choca com a mola e para momentaneamente depois de comprimir a mola . Qual é o trabalho realizado (a) pelo bloco sobre a mola e (b) pela mola sobre o bloco? (c) Qual é o valor de ? (d) Se o bloco fosse solto de uma altura acima da mola, qual seria a máxima compressão da mola?
Ver solução completaQuestão 52
(Capítulo 8.5 – Exercício 15) Uma bola de gude de é lançada verticalmente para cima usando uma espingarda de mola. A mola deve ser comprimida de exatamente para que a bola alcance um alvo colocado acima da posição da bola de gude na mola comprimida. (a) Qual é a variação da energia potencial gravitacional do sistema bola de gude-Terra durante a subida de ? (b) Qual é a variação da energia potencial elástica da mola durante o lançamento da bola de gude? (c) Qual é a constante elástica da mola?
Ver solução completaQuestão 53
(Capítulo 8.5 – Exercício 29) Um bloco de massa é apoiado em uma mola em um plano inclinado sem atrito de ângulo (Fig. 8-42). (O bloco não está preso à mola.) A mola, de constante elástica , é comprimida e depois liberada. (a) Qual é a energia potencial elástica da mola comprimida? (b) Qual é a variação da energia potencial gravitacional do sistema bloco – Terra quando o bloco se move do ponto em que foi liberado até o ponto mais alto que atinge no plano inclinado? (c) Qual é a distância percorrida pelo bloco ao longo do plano inclinado até atingir a altura máxima?
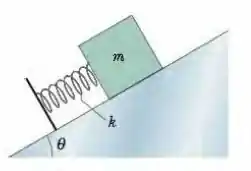
Figura 8-42 Problema 31
Ver solução completaQuestão 54
Um menino está inicialmente sentado no alto de um monte hemisférico de gelo de raio . Ele começa a deslizar para baixo com uma velocidade inicial tão pequena que pode ser desprezada (Fig. 8-45). Suponha que o atrito com o gelo seja desprezível. Em que altura o menino perde contato com o gelo?
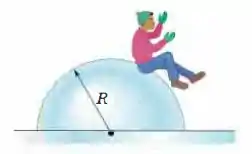
Figura 8-45 Problema 34
Ver solução completaQuestão 55
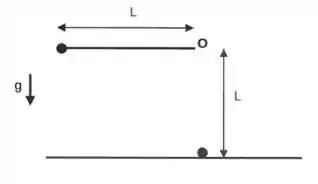
Uma bolinha de massa m está presa a uma das extremidades de uma haste rígida de massa desprezível e comprimento . A haste pode girar livremente em torno de um eixo perpendicular passando por sua outra extremidade (ponto ). O raio da bolinha é muito menor do que o comprimento da haste. O conjunto é liberado a partir do repouso na posição horizontal e, quando passa pela posição vertical, colide com uma bolinha idêntica em repouso. Não há atrito entre a bolinha e a superfície horizontal sobre a qual está apoiada. As bolinhas grudam uma na outra durante a colisão. Qual é a velocidade angular do sistema imediatamente após a colisão?
Questão 56
Considere um sistema de lançamento constituído por um plano inclinado de comprimento , inclinado de e uma mola de constante elástica . Uma das extremidades da mola está presa a um anteparo na base do plano. Na outra extremidade da mola apoiamos um bloco de massa a ser lançado. A mola tem massa desprezível e quando relaxada tem comprimento . Para lançar o bloco, a mola é comprimida até a partir da posição de equilíbrio e então o bloco é solto. Ele sobe plano acima até sair do plano fazendo uma trajetória parabólica. Existe atrito entre o plano e o bloco com . Resolva o problema utilizando somente considerações de energia.
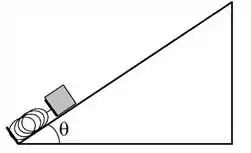
a) Determine a energia potencial elástica armazenada na mola antes do lançamento do bloco.
b) Determine a variação da energia potencial gravitacional do bloco durante a compressão da mola.
c) Suponha que quando a mola empurra o bloco plano acima, ele perde contato com a mola quando ela fica relaxada. Determine o módulo da velocidade do bloco imediatamente após ele ter perdido contato com a mola.
d) Determine a altura máxima que o bloco alcança, em relação à base do plano, depois dele ser lançado do plano inclinado numa trajetória parabólica. A velocidade do bloco na iminência de sair do plano é .
Ver solução completaQuestão 57
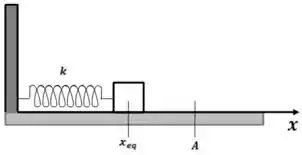
Um pequeno bloco de massa está sobre uma superfície horizontal sem atrito ligado a uma mola de constande elástica cuja outra extremidade é fixa em uma parede, como mostra a figura. O bloco é deslocado para , a partir da posição de equilíbrio, e liberado a partir do repouso. Para qualquer instante posterior, o módulo da sua velocicade é dado por:
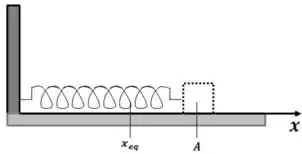
Questão 59
Um bloco de massa cai de uma determinada altura e se choca frontalmente contra a extremidade de uma mola ideal, cuja a extremidade oposta está presa no chão horizontal rígido. Selecione a alternativa que preenche corretamente as lacunas no parágrafo abaixo, na ordem em que elas aparecem.
Durante a etapa de compressão da mola, a energia cinética do bloco ............ e a energia potencial elástica armazenada no sistema massa-mola............... . No ponto de inversão do movimento, a velocidade do bloco é zero e sua aceleração é .......... .
(a) Diminui, aumenta, máxima
(b) Aumenta, diminui, zero
(c) Diminui, diminui, máxima
(d) Aumenta, diminui, máxima
(e) Diminui, aumenta, zero
Ver solução completaQuestão 60
Dois blocos de massas e estão ligados por um fio inextensível e sem massa que passa por uma polia de massa desprezível. As molas têm a mesma constante elástica . Não há atrito no eixo da polia nem entre o bloco de massa e a superfície horizontal. Se os blocos são liberados a partir do repouso com ambas as molas relaxadas, qual é a distância que o bloco que está sobre a superfície horizontal percorre até parar pela primeira vez?
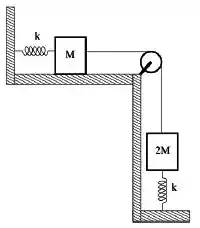
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 61
Um bloco de se move com uma velocidade de sobre uma superfície horizontal sem atrito, dirigindo-se contra uma mola cuja constante elástica é dada por e que possui uma de suas extremidades presa a uma parede (ver figura abaixo).
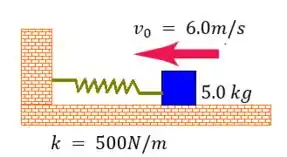
b) Se a distância máxima que a mola pudesse ser comprimida fosse de , qual seria o valor máximo de ?
Ver solução completaQuestão 63
PARTE I
Um bloco de massa desliza por uma rampa sem atrito com inclinação e comprimento total de iniciando o movimento a partir do repouso. Ao longo da rampa existe uma mola de constante elástica que se encontra a uma distância abaixo do bloco. O bloco atinge o repouso ao comprimir a mola de uma distância . Considere .
(a ) Escreva a equação literal para a conservação da energia mecânica para as posições inicial e final do movimento em função dos dados do problema.
(b ) Determine a compressão da mola quando a aceleração do sistema for zero.
(c ) Obtenha o módulo da velocidade máxima que o bloco alcança durante a descida.
PARTE II:
Em um salto de pára-quedas o atleta abandona o avião com velocidade vertical . Considerando a resistência do ar, sua velocidade horizontal inicial se torna nula imediatamente ao abandonar a aeronave e pode ser desprezada nos cálculos, deste modo podemos considerar uma trajetória de queda estritamente vertical. O saltador chega ao chão com velocidade
Calcule a energia total dissipada pela resistência do ar no conjunto saltador + pára-quedas. Dados: ; massa total do saltador + pára-quedas igual à ; altura inicial do avião . Use o referencial indicado com no solo.
Ver solução completaQuestão 64
Um carrinho de massa se encontra preso através de um fio e comprimindo uma mola, conforme indica a figura. Estudos prévios indicam que se o fio se romper, o carrinho é lançado com uma velocidade de . Neste caso, podemos afirmar que a energia potencial elástica armazenada na mola vale:
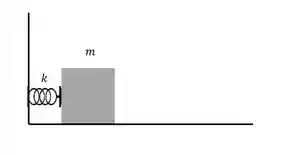
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 65
Um famoso experimento proposto por Galileu consiste em dois objetos de massas diferentes (uma pena e um martelo, por exemplo) largados simultaneamente a partir do repouso desde uma altura em relação ao solo. Considere que este experimento seja realizado em uma grande câmara de vácuo em um laboratório na superfície da Terra, e sejam e as massas dos dois objetos, onde . Analise as seguintes afirmações a respeito deste experimento:
I) À medida que cada objeto descreve o movimento de queda livre, sua energia cinética aumenta de quantidades iguais durante distâncias percorridas iguais.
II) O trabalho realizado pela força gravitacional durante a queda livre é menor sobre o objeto de massa .
III) Ao tocar o solo, ambos os objetos possuem a mesma energia cinética.
IV) Ao tocar o solo, a energia cinética do objeto de massa vale .
São CORRETAS as afirmações:
(A) I, II e IV
(B) I, III e IV
(C) III e IV
(D) I, II e III
(E) I, II, III e IV
Ver solução completaQuestão 66
Um bloco de massa está se movendo inicialmente para a direita, sobre uma superfície horizontal sem atrito, com velocidade . Ele então comprime uma mola de constante elástica . Durante a compressão, qual o comprimento da mola para que sua energia potencial seja igual a energia cinética do bloco?
a)
b)
c)
d)
e)
Ver solução completa