136- Uma mola de constante elástica é mantida na posição vertical, com a extremidade inferior sustentada por uma superfície horizontal. A extremidade superior é comprimida 25 cm, e um bloco com peso de 50 N é colocado sobre a mola, e o sistema é liberado.
Supondo que a energia potencial gravitacional do bloco é zero no ponto (y = 0) em que o sistema é liberado, determine a energia cinética K do bloco para y igual a (a) 0, (b) 0,050 m, (c) 0,10 m, (d) 0,15 m, (e) 0,20 m. (f) Calcule também o valor de y para a altura máxima atingida pelo bloco.
Passo 1
Quando o sistema massa-mola é liberado o mesmo tende a oscilar seguindo a trajetória representada no desenho abaixo.
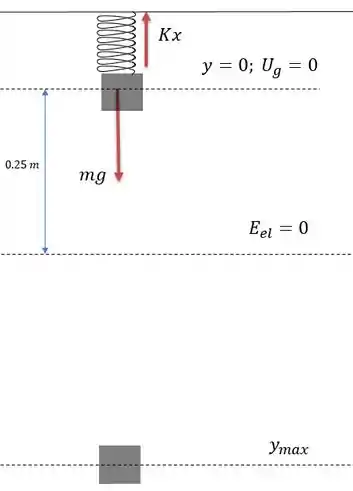
Pela conservação temos, a energia no bloco no instante que ela é liberada e em um depois:
No começo da a mola está em e como dito na questão isso significa que a energia potencial gravitacional também vale , como o bloco não se movimenta então a energia cinética vale 0 também, tendo somente a energia elástica como componente de energia. Então a energia mecânica total vale:
Logo escrevendo a equação da energia mecânica para um tempo depois da posição inicial nós teremos:
Outra coisa importante é como vamos supor positivo a medida que ele ‘cai’, logo só terá valores positivos.
Passo 2
Isolando a energia cinética temos:
Substituindo os valores temos:
- Para :
- Para :
- Para :
- Para :
- Para
- Para encontrar o máximo valor de temos que simplesmente entender o sistema. Nos extremos do sistema a energia cinética é nula sobrando apenas a energia potencial gravitacional e a energia potencial elástica em um que desconhecemos completamente, assim ficando:
Passo 3
Substituindo os valores temos:
Isso nos dá uma equação do segundo grau igual a:
Com essa equação encontraremos:
, como era de se esperar.
Como é esperado encontramos uma das raízes na origem, a outra posição portanto será o ponto de