Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 81
Ossos e músculos. O braço de um paciente em tratamento pesa 20,5 N e ergue-se a um peso de 112,0-N. Essas duas forças têm direção verticalmente para baixo. As únicas outras forças significativas no braço dele vêm do músculo do bíceps (que age perpendicularmente ao braço) e do cotovelo. Se o bíceps produz uma tração de 232 N, quando o braço é levantado a 43º em relação ao plano horizontal, descubra o módulo e a direção da força que o cotovelo exerce sobre o braço. (A soma das forças do cotovelo e do bíceps deve equilibrar o peso do braço e o peso que ele carrega, de modo que a soma vetorial deve ser 132,5 N, para cima.)
Passo 1
E aí, galerinha!
Temos aqui mais uma questão de soma vetorial. Dessa vez temos que achar o módulo e a direção da força do cotovelo para que .
A gente só precisa decompor as forças em x e em y e usar o maravilhoso Teorema de Pitágoras pra encontrar a força de . A direção a gente vai encontrar através da tangente do ângulo que o cotovelo faz com o eixo x.
Então bora lá!
Passo 2
Vamos começar fazendo um desenho:
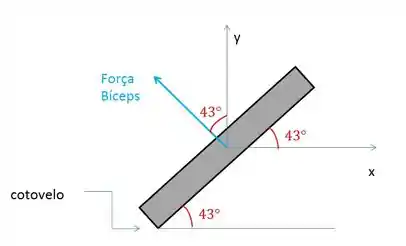
decompondo as forças em :
E ,então:
Agora em :
Tranquilo até aqui?
Passo 3
Agora que temos as componentes, vamos usar o lindo, o maravilhoso, o extraordinário Teorema de Pitágoras pra achar o módulo da força exercida pelo cotovelo. XD
Achamos o módulo \O/
Legal, né?
Passo 4
Agora vamos encontrar o ângulo que o cotovelo faz com o eixo -Ox e pra isso vamos usar a tangente:
Agora só falta usar o arco-tangente pra encontrar o ângulo:
E acabamos por aqui! Entendeu tudo? Responde Aí! 😊
Resposta
Módulo:
Direção: em relação ao eixo -Ox