Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 33

Uma mosca pousa na parede de um quarto. O canto inferior esquerdo da parede é selecionado como a origem de um sistema de coordenadas cartesianas bidimensional. Se a mosca estiver localizada no ponto com coordenadas ( 2,00 ,   1,00 )   m :

a) a que distância ela está da origem?

b) Qual é a localização em coordenadas polares?

Passo 1

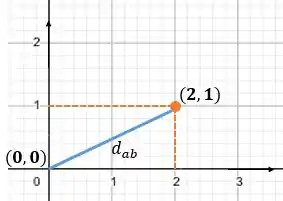
Eai pessoal. Bora resolver mais uma questão? A mosca está no ponto ( 2,1 ) em relação a origem, como mostra na imagem a seguir.

  1. Conhecemos a distância através da diferença entre os pontos. Quando colocamos esses pontos em um plano cartesiano é necessário aplicar o TEOREMA DE PITÁGORAS.

Aquela equação que todos nós amamos.

Considerando os dois pontos na reta, podemos usar o Teorema de Pitágoras para encontrar a distância entre esses pontos.

d a b = ( x b - x a ) ² + ( y b - y a ) ²

Vamos considerar o ponto A   ( 0,0 ) e o ponto   B   ( 2,1 ) . Substituindo

d a b = 2 - 0 2 + 1 - 0 2

d a b = 2 2 + 1 2

d a b = 4 + 1

d a b = 5

Passo 2

  1. As coordenadas cartesianas são representadas por ( x , y ) e as coordenadas polares por ( r , θ ) .

x = r c o s θ

y = r   s e n θ

Encontrando o valor de r para ( 2,1 )

r = x 2 + y 2              

r = ( 2 ) 2 + ( 1 ) ²

r = 4 + 1

r = 5

Podemos usar a seguinte relação

x ,   y = r c o s θ , r s e n θ

2 ,   1 = r c o s θ , r s e n θ

Encontrando θ

x = r c o s   θ

x cos ⁡ θ = r

y = r s e n θ

y sen ⁡ θ = r

Igualando as equações.

x cos ⁡ θ = y sen ⁡ θ

s e n   θ cos ⁡ θ = y x

t g   θ = y x

t g   θ = 1 2

θ = arctan ⁡ 1 2

A coordenada cartesiana é ( 5 ,   arctan ⁡ 1 2 )

Resposta

  1. d a b = 5
  2. ( 5 ,   arctan ⁡ 1 2 )
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use um diagrama em escala para determinar os componentes x e y dos vetores seguintes. Para cada vetor, os números indicam o módulo do vetor e o ângulo que ele faz com o eixo + O x medido supondo-se um
O vetor A possui componentes A x = 1,30c m , A y = 2,25c m ; o vetor B possui componentes B x = 4,10c m , B y = – 3,75c m . Ache a) os componentes da soma vetorial A → + B → ; b) o módulo e a direção
O vetor possui comprimento igual a 2,80c m e está no primeiro quadrante a 60,0 ° acima do eixo O x . O vetor possui comprimento igual a 1,90c m e está no quarto quadrante a 60,0 ° abaixo do eixo O x (
O vetor possui comprimento igual a 2,80c m e está no primeiro quadrante a 60,0 ° acima do eixo O x . O vetor possui comprimento igual a 1,90c m e está no quarto quadrante a 60,0 ° abaixo do eixo O x (
Um professor de física desorientado dirige 3,25k m do sul para o norte, depois4,75k m de leste para oeste e a seguir 1,50k m do norte para o sul. Determine o módulo, a direção e o sentido do deslocame