Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 1.Problemas - Ex. 38
O vetor tem componentes , e de , e unidades, respectivamente. Calcule
a) o módulo de
b) o ângulo que forma com cada eixo de coordenadas
Passo 1
- Para calcular o módulo de B, devemos aplicar o Teorema de Pitágoras.
- Vamos calcular vãos utilizar a seguinte equação.
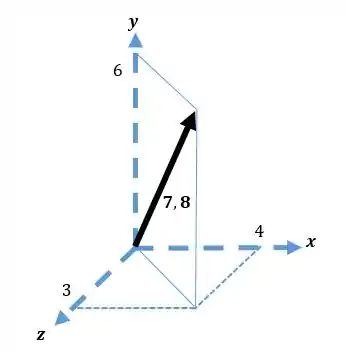
Passo 2
1° com o plano :
2° com o plano :
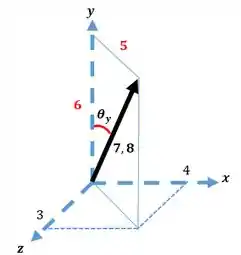
3° com o plano :
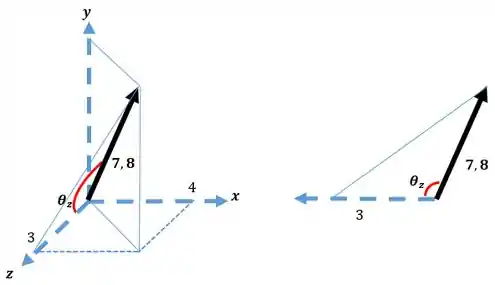
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
a) Escreva cada vetor indicado na Figura 1.37 em termos dos vetores unitários i e j. b) Use os vetores unitários para escrever o vetor C, onde C=3a - 4b. c) Encontre o módulo e a direção de C.
Duas cordas em um plano vertical exercem as mesmas forças de módulo sobre um peso suspenso, mas a tração entre elas possui um ângulo de 86,0 ° . Qual é a força de tração que cada uma exerce, se a traç
c) Se A → = a 3,0i ^ + 4,0j ^ , onde a é uma constante, determine o valor de a que torne umvetor unitário.
Em cada caso, determine os componentes de x- e y- do vetor A → : a) A → = 5,0i ^ - 6,3j ^ ; b) A → = 11,2 j ^ - 9,91 i ^ ; c) A → = - 15,0i ^ + 22,4j ^ ; d) A → = 5,0 B ^ , onde B ^ = 4i ^ - 6j ^ .
Dados dois vetores A → = 4,0i ^ + 3,0j ^ e B → = 5,0i ^ - 2,0j ^ . a) ache o módulo de cada vetor; b) escreva uma expressão para a diferença vetorial A → - B → usando vetores unitários; c) ache omódul