Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 8.1 - Ex. 20
20. Uma zarabatana dupla é mostrada na figura 8-41. O ar é soprado no lado esquerdo, e duas ervilhas idênticas e estão colocadas dentro de cada canudo, como mostrado. Se a zarabatana é mantida na horizontal, enquanto as ervilhas são lançadas, qual das ervilhas, ou , será atirada para mais longe após abandonar a zarabatana? Explique! (Use como base de sua argumentação, o teorema do impulso-quantidade de movimento)
Passo 1
Olá, querido! Cê tá bem?
Então, vamos entender aí o que está acontecendo. Imagina que você tem essa zarabatana. E você quer atirar essas bolinhas dentro dela. O que você faz? Você assopra! Um esqueminha:
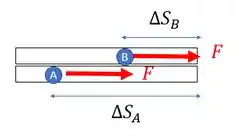
Você assopra pela extremidade esquerda. Então o que acontece é que isso gera uma força em cada bolinha, fazendo com que elas se movam até a outra extremidade da zarabatana.
Sacou o funcionamento dessa bonita? Agora o que a gente quer é saber se a bolinha ou a vai atingir uma distância maior quando sair do caninho.
E para responder essa a gente considera
E ele pede para usar teorema do impulso-quantidade de movimento. Bora ver como responder essa!
Passo 2
Bom! Já que o objetivo é resolver a questão usando como base o teorema do impulso-quantidade de movimento, vamos então à fórmula desse teorema, que tem a seguinte cara:
Essa cara está muito feia né? Vamos considerar que a força sobre as ervilhas (bolinhas) é constante. Aí essa integral vira:
Podemos lembrar que . E a gente pode pensar que essa variação de quantidade de movimento é dada por . Então o teorema fica:
Onde é o impulso resultante, é a força sobre cada bolinha, é o tempo de atuação da força, ou seja, é o tempo em que a bolinha dentro da zarabatana, é a massa de uma bolinha e é o aumento de velocidade que uma bolinha sofre antes de sair do cano.
Passo 3
Agora vamos refletir.
Nos problemas de lançamento de projeteis, quanto maior fosse a velocidade inicial do projetil maior era o alcance dele.
O que acontece com uma bolinha é que ela é lançada assim que sai do cano. Então a velocidade inicial de lançamento dela é a velocidade que ela tem ao sair do cano.
Então, a bolinha que sair com maior velocidade do cano é a que vai ter maior alcance. E a pergunta que não quer calar é: qual ervilha tem maior velocidade ao sair do cano?
Aí que entra o teorema:
Por esse teorema, quanto maior o tempo de contato , do corpo em questão, quando submetida a uma força, maior será a variação de velocidade. No nosso exercício, as duas ervilhas estão submetidas à mesma força (mesma aceleração), originada do sopro.
Entretanto, como o ar é soprado no lado esquerdo, a ervilha em , tem um tempo de contato maior com a força do que a ervilha em , isso porque percorre uma distância maior para sair da zarabatana.
Logo, a ervilha irá adquirir ter uma variação de velocidade maior e consequentemente, terá a maior velocidade ao sair do cano, e assim será atirada mais longe.
Resposta
A ervilha será atirada mais longe.