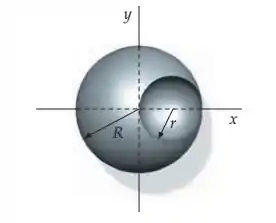
Uma esfera maciça de raio tem o centro na origem. Ela tem uma massa específica uniforme de massa , exceto pelo fato de possuir uma cavidade esférica de raio centrada em , como na figura. Determine o campo gravitacional nos pontos do eixo com . Dica: A cavidade pode ser pensada como uma esfera de massa , mais uma esfera de massa “negativa” .

A idéia aqui, pessoa, é a seguinte: A gente vai olhar pra essa esfera com a cavidade e encher ela como uma esfera inteira, com uma esfera menor faltando dentro dela. “Ué, mas isso é óbvio, não é isso que é um buraco?” Sim, meu jovem Padawan, é pra acharmos o campo gravitacional dessa esfera esburacada, podemos somar o campo gravitacional da esfera toda com o campo gravitacional do buraco, considerando o campo do buraco como um “anti-campo”, de sinal negativo. Vai ficar assim: