Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 25

Uma bola de 50 g é lançada do nível do solo com um ângulo de 30° acima da horizontal. A velocidade inicial é de 25 m/s.

  1. Quais são os valores de p x e p y um instante após a bola ser lançada, no ponto de altura máxima, e um instante antes da bola atingir o solo?
  2. Por que um dos componentes de p → é constante? Explique.
  3. Para o componente de p → que é variável, mostre que a variação do momento é igual à força gravitacional sobre a bola multiplicada pelo tempo de voo. Explique por que isso ocorre desta maneira.

Passo 1

Temos um lançamento oblíquo que pode ser esquematizado da seguinte maneira.

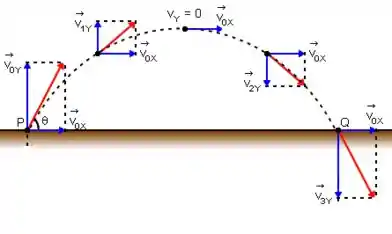
Note que há apenas a força gravitacional agindo para baixo. Assim, a velocidade em x deve ser constante ao longo de todo o movimento, enquanto que o movimento em y é um movimento uniformemente acelerado.

Passo 2

  • Logo após lançar a bola, temos:

    • v → = v 0 x i ^ + v o y j ^ = v 0 cos ⁡ θ i ^ + v 0 sin ⁡ θ j ^

    v → = 25 ⋅ cos ⁡ 30 ° i ^ + 25 ⋅ sin ⁡ 30 °   j ^ = 21,6   i ^ + 12,5   j ^   m / s

    Portanto, temos (lembre-se que 50 g equivalem a 0,05 kg)

    p → = m v → = 0,05   k g 21,6   i ^ + 12,5   j ^ = 1,08   i ^ + 0,63   j ^   k g   m / s

  • No ponto de altura máxima, temos apenas a componente horizontal da velocidade:

v → = v x i ^ = 21,6   i ^   m / s  

∴ p → = m v → = 0,05   k g 21,6   i ^ = 1,08   i ^   k g   m / s

Antes de calcularmos p → para o um instante antes da bola atingir o solo, vamos relembrar uma das propriedades do movimento parabólico. Na figura acima, temos que

v → 3 y = - v → 0 y

Portanto, a quantidade de movimento p → será exatamente igual à que já calculamos para logo após lançar a bola, bastando apenas trocar o sinal da velocidade y .

p → = 1,08   i ^ - 0,63   j ^   k g   m / s

Passo 3

  • A quantidade de movimento em x permanece constante, já a velocidade em x é constante (não há força na direção x )

    • Passo 4

  • A força em y é constante. Assim, o impulso da força peso será:

    • I y = m g ⋅ Δ t

    onde Δ t é o tempo em que a bola fica no ar. Pelo teorema do impulso, temos

    Δ p y = I y ⟹ Δ p y = m g ⋅ Δ t

    que é o que queríamos demonstrar.

    Resposta

    Ei, a resposta está no passo a passo :)

    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    Uma bala de 10g é disparada contra um bloco de madeira de 10k g em repouso sobre uma mesa de madeira. Com a bala incrustada nele, o bloco desliza por 5c m sobre a mesa. Qual era o valor da velocidade
    Uma bola de argila de 20g desloca-se para leste a 2,0m / s quando colide com outra bola de argila de 30g que se desloca com a orientação de 30 ° sudoeste a 1,0m / s . Qual é o módulo e qual é a orient
    O isótopo do carbono 14 C é usado para realizar datação de artefatos arqueológicos por meio do carbono. O 14 C (massa de 2,34 ×10 - 26k g ) decai pelo processo conhecido como decaimento beta, em que o
    Um próton (massa de 1 u) é lançado com uma velocidade de 5,0 ×10 7m / s em direção a um alvo de ouro. O núcleo de um átomo de ouro (massa de 197 u) repele o próton e o desvia diretamente para trás, em
    O núcleo do isótopo do polônio 214P o (massa de 214 u) é radioativo e sofre decaimento emitindo uma partícula alfa (um núcleo de hélio com massa de 4 u). Através de experimentos de laboratório, mede-s