Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 28

28. Você enxerga o rapaz da porta ao lado tentando descer um caixote para a rua empurrando-o. Ele mal consegue mantê-lo em movimento, e seus pés de vez em quando escorregam sobre o piso. Você começa a se indagar quão pesado é o caixote. Você, então, chama o rapaz e pergunta-lhe qual é sua massa, ao que ele responde “ 50   k g ” . Baseado em suas recentes aulas de física, você estima que os coeficientes de atrito estático e cinético valem, respectivamente, 0,80 e 0,40 para os sapatos do rapaz, e 0,5 e 0,2 para o caixote. Estime, agora, a massa do caixote.

Passo 1

Então galera nesse problema teremos que usar o que aprendemos até agora das leis de Newton. Primeiro vamos fazer um diagrama de corpo livre do rapaz e da caixa para analisarmos essa situação melhor.

Mas antes de irmos para o diagrama temos que nos atentar no detalhe crucial para esse problema, que envolve a terceira lei, que a força que o rapaz faz na caixa para empurrá-la é a mesma que a caixa faz no rapaz.

Outro detalhe é que esse sistema está em equilíbrio então a soma das forças na direção x e na direção y é zero, logo a força resultante (segunda lei) é zero nessas direções, assim temos o seguinte:

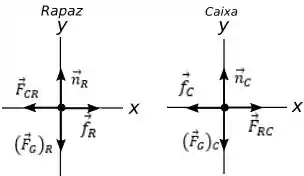
Para encontrar a massa da caixa teremos que analisar a segunda lei para o rapaz e para caixa na direção y e na direção x para encontrarmos expressões para a força que caixa faz no rapaz e a força que o rapaz faz na caixa que dependam das massas.

Descobrindo essas expressões vamos usar a terceira lei, pois assim temos que:

F R C = F C R

Com isso vamos conseguir isolar a massa da caixa e achar seu valor.

Passo 2

Vamos então começar analisando a caixa.

Na direção y temos o seguinte:

n C - F G C = 0

⇒ n C = F G C

Lembrando que a força gravitacional é dada por F G = m g , temos que:

n C = m C g

Na direção x temos o seguinte:

F R C - f C = 0

Onde essa força de atrito é cinético já que a caixa está se movendo um pouco, assim:

F R C = f C

⇒ F R C = μ c C n C

Usando o que achamos para n C temos:

F R C = μ c C m C g

Passo 3

Vamos agora analisar o rapaz.

Na direção y temos o seguinte:

n R - F G R = 0

⇒ n R = F G R

⇒ n R = m R g

Na direção x temos o seguinte:

F C R - f R = 0

Onde essa força de atrito é estático máximo já que o rapaz de vez em quando escorrega tentando empurrar a caixa, logo ele atinge o atrito estático máximo, assim:

F R C = f R

⇒ F C R = μ e R n R

Usando o que achamos para n R temos:

F C R = μ e R m R g

Passo 4

Agora como sabemos temos que:

F C R = F R C

Assim temos que:

μ e R m R g = μ c C m C g

Isolando m C temos que:

m C = μ e R m R μ c C

Substituindo o que sabemos, temos:

m C = ( 0,8 ) ( 50 ) 0,2

= 40 0,2

⇒ m C = 200   k g

Resposta

m C = 200   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os Exercícios de 1 a 6 descrevem, cada um, uma situação. Em cada um:a. Seguindo os passos do Box Tático 7.1, desenhe um diagrama de interação.b. Identifique o “sistema” em seu diagrama de interação.c.
Os Exercícios de 1 a 6 descrevem, cada um, uma situação. Em cada um:a. Seguindo os passos do Box Tático 7.1, desenhe um diagrama de interação.b. Identifique o “sistema” em seu diagrama de interação.c.
53. A FIGURA PD7.53 mostra um hamster de 200 g parado sobre a rampade um bloco em cunha de 800 g. O bloco, por sua vez, repousa sobreuma balança de banheiro.a. Inicialmente, o atrito estático é sufici
Os Exercícios de 1 a 6 descrevem, cada um, uma situação. Em cada um:a. Seguindo os passos do Box Tático 7.1, desenhe um diagrama de interação.b. Identifique o “sistema” em seu diagrama de interação.c.
Os Exercícios de 1 a 6 descrevem, cada um, uma situação. Em cada um:a. Seguindo os passos do Box Tático 7.1, desenhe um diagrama de interação.b. Identifique o “sistema” em seu diagrama de interação.c.