Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 53
53. A FIGURA PD7.53 mostra um hamster de 200 g parado sobre a rampa
de um bloco em cunha de 800 g. O bloco, por sua vez, repousa sobre
uma balança de banheiro.
a. Inicialmente, o atrito estático é suficiente para impedir o hamster
de escorregar. Neste caso, o hamster e o bloco constituem, efetivamente,
uma única massa de 1.000 g, e a balança deve marcar
9,8 N. Mostre que este é o caso tratando o hamster e o bloco
como objetos separados e analisando as forças envolvidas.
b. Um óleo lubrificante extrafino com !e " !c " 0 é espalhado sobre
a superfície superior do bloco, fazendo com que o hamster
escorregue para baixo. O atrito entre o bloco e a balança é suficientemente
grande para que o bloco não escorregue sobre a balança.
Quanto marca a balança agora, enquanto o hamster desce
a rampa?
Passo 1
a)
Esse tipo de exercício a gente só precisa fazer com calma e cuidar bem quais são as forças que estão atuando no hamster e na cunha que tudo vai dar certo.
Vamos fazer o diagrama de corpo livre do hamster:
Como sabemos a massa do hamster, podemos calcular a força gravitacional que atua sobre ele:
Agora vamos decompor esse vetor em e em e montar as equações de cada um desses eixos. Em :
E em :
Agora vamos montar as equações em cada um dos eixos. Como o sistema esta parado não teremos aceleração em nenhum dos eixos.
Em :
Agora vamos montar a equação para :
Passo 2
Agora que já temos o valor das forças que atuam sobre o hamster podemos montar o diagrama de corpo livre da cunha.
A mesma força normal que a cunha aplica sobre o hamster o hamster vai aplicar sobre a cunha, a mesma coisa para o atrito. Então o diagrama da cunha fica assim:
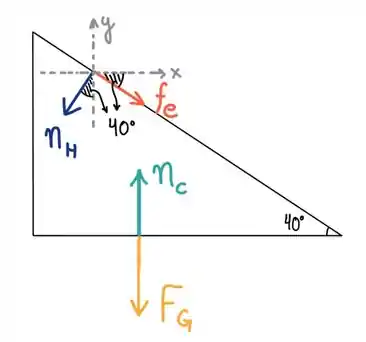
O peso medido pela balança é igual a normal que ela aplica sobre a cunha, ou seja, precisamos encontrar o valor de . Vamos as contas, primeiro precisamos decompor as forças que o hamster aplica na cunha.
e
A soma de todas as forças no eixo é igual a zero:
Substituindo algumas coisinhas:
Temos todos esses valores, substituindo tudo isso:
Fazendo as continhas:
Agora pra descobrir qual é massa medida pela balança só precisamos dividir o peso pela aceleração da gravidade:
Tudo certinho, como deveria ser.
Passo 3
b)
Agora a gente não tem mais atrito entre o hamster e a cunha. Porém isso não vai mudar a normal do hamster, pois a equação que montamos lá em cima com o eixo do hamter continua igual. Então:
Agora só precisamos montar a equação para o eixo da cunha. A normal do hamster permanece a mesma e o peso da cunha também mas agora a gente não tem mais a força de atrito, então a equação fica:
Isolando a normal da cunha:
Substituindo os valores:
Fazendo as continhas:
Dividindo pela gravidade para encontrar a massa:
Resposta
b)