Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 41
41. O livro de física de da FIGURA P7.41 está ligado por um barbante a uma caneca de café de . Dá-se um pequeno empurrão no livro para cima e ele é liberado com uma velocidade de . Os coeficientes de atrito são e .
Que distância o livro subirá deslizando?
No ponto mais alto, o livro fica grudado na rampa ou ele desliza de volta para baixo?
Passo 1
Então galera, para resolver o item , temos que analisar nosso sistema enquanto ele está em movimento utilizando a segunda lei de Newton, pois assim encontramos a aceleração com que o livro é freado na rampa.
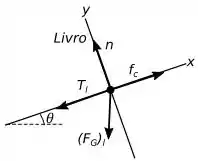
Para nossa vida ficar mais fácil vamos montar um diagrama de corpo livre para essa situação, temos o seguinte:
Desse diagrama podemos dizer que , já que eles estão presos por uma corda ideal.
Achando a aceleração podemos encontrar quanto o livro andou com a seguinte equação da cinemática.
Onde iremos querer achar .
Para responder o item vamos montar um diagrama de corpo livre para o livro no caso que ele está em repouso e encontrar o valor da força de atrito, usando a segunda lei de Newton, que faz com que ele fique parado. Temos o seguinte diagrama:
Caso essa força seja maior do que a força de atrito máximo que podemos calcular para o livro usando o coeficiente de atrito estático, assim:
Passo 2
Vamos resolver o item , vamos começar analisando a caneca.
Para caneca só precisamos analisar a direção , temos:
Agora vamos analisar o livro primeiro na direção , temos:
Agora vamos analisar para direção , temos:
Usando o que encontramos para a normal , temos:
Passo 3
Agora como sabemos do passo temos que , então somando as duas expressões que chegamos no passo anterior temos:
Então temos que:
Agora vamos substituir tudo o que sabemos, assim temos:
Então temos que:
Passo 4
Agora que temos a aceleração podemos encontrar a distância que o livro percorreu até parar, temos:
Substituindo o que sabemos, temos:
Então temos que:
Passo 5
Agora vamos resolver o item , onde vamos analisar o livro para e ver a força de atrito estático necessária para manter o livro para, temos o seguinte:
Já sabemos que e do desenvolvimento de , encontramos que:
Assim temos que:
Isolando , temos:
Substituindo o que sabemos, temos:
Então essa a força de atrito necessária para manter o livro em repouso.
Agora vamos usar a equação da força de atrito estático máximo para saber a força máxima que esse livro pode ter de atrito, temos:
Substituindo tudo o que sabemos, temos:
Como a força máxima de atrito que livro pode ter é menor que a força de atrito necessária para mantê-lo em repouso o nosso livro acaba descendo a rampa.
Resposta
O livro desliza para baixo.