Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 40
40. Uma caixa de , sobre uma rampa sem atrito e inclinada em 35°, está ligada a um peso de suspenso, através de um barbante de massa desprezível que passa por uma polia, também sem massa e livre de atrito. O desenho da situação é semelhante ao da Figura P7.39.
- Quanto vale a tensão na corda quando a caixa de é mantida no lugar e não pode se mover?
- Se, então, a caixa for liberada, de que maneira ela se moverá na rampa?
- Quanto vale a tensão na corda uma vez que a caixa tenha começado a deslizar?
Passo 1
Nesse exercício é fundamental analisar e aplicar as Leis de Newton então precisamos lembrá-las:
Primeira Lei – Um objeto permanecerá em repouso ou continuará movendo-se com velocidade constante (equilíbrio) se e somente se
Segunda Lei –
Terceira Lei –
Vamos também desenhar o diagrama de força tanto da caixa quanto da caixa pois assim podemos ver que forças agem sobre cada caixa de forma explícita.
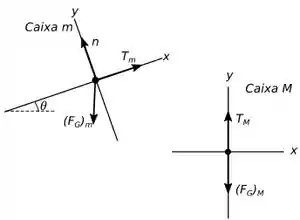
Agora que as leis estão frescas na nossa cabeça e temos nosso diagrama vamos com calma que eu vou explicar tudinho para você!
Passo 2
A grande sacada inicial que temos que ter esse exercício é olhar o diagrama de forças e ver que podemos usar a terceira Lei de Newton de forma muito eficiente. Mas como ela vai nos ajudar a descobrir quem é a tração da corda ?
A força (de tensão) que a corda faz na caixa é a mesma (com sentido oposto) que caixa faz na corda.
A força (de tensão) que a corda faz na caixa é a mesma (com sentido oposto) que caixa faz na corda.
Sendo assim, podemos afirmar que:
Então, basta achar ou para saber quem é .
Olhando o diagrama de forças podemos ver que é muito mais fácil de achar então, usando a segunda Lei de Newton, sabemos que:
E agora? Bom, por não ter atrito da caixa com a rampa quando a caixa for solta haverá movimento para um dos lados e isso fará a caixa se mover também.
Contudo, esse item pede a tensão da corda quando a caixa NÃO se move, ou seja, o sistema está sendo “segurado”, e se isso acontece ele está em equilíbrio.
Se o sistema está em equilíbrio, de acordo com a primeira lei, sabemos que:
Agora podemos resolver.
Passo 3
Juntando tudo o que chegamos no passo anterior temos que:
Substituindo o que temos:
Ou seja:
Passo 4
A caixa poderá subir ou descer a rampa, porém vamos descobrir o que ela fazendo a partir da aceleração (se positiva ou negativa) então iremos usar novamente a Lei de Newton mas aqui vem a particularidade pois ambas as caixas estão em movimento, sendo assim:
Como as caixas vão se mover então há apenas dois movimentos possíveis: Se está subindo, está descendo ou se está descendo, está subido e a partir disso podemos afirmar que elas possuem a mesma aceleração, porém com sentido oposto. Podemos dizer que:
Nossas equações ficam na forma:
Igualando as duas equações:
Estamos pertinho do resultado, vamos lá.
Passo 5
Agora nos basta isolar o já que é o valor que queremos.
Agora vamos substituir todos os valores que temos:
, ou seja, a caixa acelera para cima.
Passo 6
Esse item vai ficar fácil de resolver pois no Passo 4 encontramos duas equações para encontrar o em movimento, é só escolher a mais simples e substituir os valores que temos, ou seja:
Pronto, resolvemos tudo!
Resposta