Enunciado
Física - Halliday - Vol 3- Ed: 8º - Capítulo 29.2 - Ex. 29
Na figura 29-57 mostra, em seção reta, dois fios retilíneos muito longos, ambos percorridos por uma corrente de orientada para fora do papel. A distância entre os fios é e a distância entre o ponto , equidistante dos dois fios, e o ponto médio do segmento de reta que liga os dois fios é . Determine o módulo do campo magnético total produzido no ponto pelos fios.
Passo 1
E aí, galerinha!! Tudo certinho? 😉
Nesse problema temos dois fios paralelos, separados por uma distancia e ambos percorridos por uma corrente . A partir daí queremos obter o modulo do campo magnético no ponto cituado a do ponto medio de .
Parece complicado? 👀
Vamos primeiro lembrar que o campo elétrico gerado por um fio paralelo é dado pela seguinte equação para o fio .
E pela seguinte equação para o fio .
Podemos então analisar a direção desse campo olhando a simetria do problema.
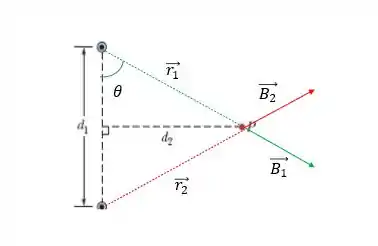
Analisando essa simetria, a gente pode ver que os campos se anulam na vertical gerando uma resultante para a direita!
Sacou? Bora começar! 😉
Passo 2
O enunciado nos disse que os fios estão simétricos e tem a mesma corrente no mesmo sentido então temos que:
E como a equação do campo só depende dessas variáveis:
Logo:
o campo resultante será:
Agora vamos então calcular a distância
E também o ângulo
Tranquilo até aqui? 😁
Passo 3
Assim podemos substituir geral na equação:
Substituindo as variáveis...
E aí! entendeu tudo? Responde Aí! 😁
Resposta
O módulo do campo magnétigo no ponto P é: