Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 27.1 - Ex. 27
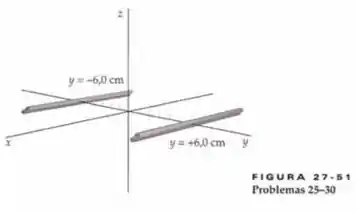
A corrente no fio em está na direção e a corrente no fio em está na direção . Determine o campo magnético nos seguintes pontos do eixo .
Passo 1
E aí bonit@s, tudo bem com vocês? Preparados pra mais uma questão?
Se liga só, vamos denotar como positivo o fio (e a corrente) em e como negativo o fio (e a corrente) em . Podemos usar para encontrar o campo magnético devido a cada um dos fios condutores de corrente e sobrepor os campos magnéticos devido às correntes nesses fios para encontrar nos pontos dados no eixo . Podemos aplicar a regra da mão direita para encontrar a direção de cada um dos campos e, portanto, de .
Passo 2
Para o primeiro item, temos o campo magnético resultante em dado por
Agora, vamos encontrar as magnitudes dos campos magnéticos devido a cada fio que serão dados por
E
Aplicando a regra da mão direita teremos
E
Dessa forma, teremos como campo resultante
Passo 3
Para o segundo item usaremos a mesma ideia, de tal forma que encontraremos
Calculando separadamente teremos
Aplicando a regra da mão direita vamos encontrar
Sendo, assim nosso campo resultante será
Passo 4
Já para o terceiro item não será tão fácil assim, mas procederemos da mesma forma fizemos para o item com a diferença de que os sinais irão mudar
Onde
E
Então vamos ter
Passo 5
Por fim, vamos proceder da mesma forma, porém, agora para . Assim, nós encontraremos
Dessa forma, teremos como campo magnético resultante
Pronto, tá finalizado nosso exercício.