Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Exercício - Ex. 7
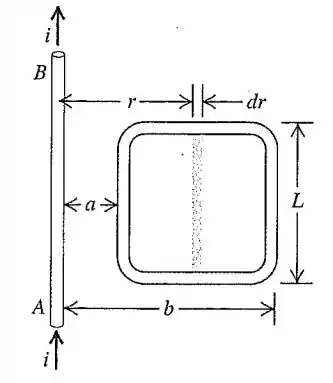
29.7. A corrente no fio longo e retilíneo AB indicado na figura 29.27 está orientada de baixo para cima e aumenta regularmente a uma taxa . (a) No instante em que a corrente é i, quais são o módulo, a direção e o sentido do campo a uma distância r para a direita do fio? (b) Qual é o fluxo através da faixa estreita e sombreada? (c) Qual é o fluxo total através da espira? (d) Qual é a fem induzida na espira? (e) Avalie o valor numérico da fem induzida, se a=12,0 cm, b=36,0 cm, L=24,0 cm e
Passo 1
Bom, primeiro podemos calcular o módulo do campo magnético, e para isso podemos usar a equação
A corrente é
Então
E para descobrir o sentido e a direção do campo magnético podemos usar a regra da mão direita. Sendo assim seu sentido e direção são para dentro da página. Essa é a resposta do item (a).
Passo 2
Agora vamos para o item (b). Vamos calcular o fluxo pela faixa. Bom, sabemos que o fluxo é calculado por
Mas queremos a diferencial, então
Bom, podemos calcular com os dados do desenho
E o módulo do campo magnético nós calculamos no item anterior
Então
Passo 3
Agora no item (c), para calcular o fluxo total, só precisamos integrar a resposta do item anterior, ou seja
Então vamos integrar
Vamos colocar as variáveis para fora da integral
Fazendo essa integral
Passo 4
No item (d) agora, devemos calcular a força eletromotriz induzida na espira. Bom a fem é a variação do fluxo magnético em relação ao tempo, então
Bom agora a gente vai precisar fazer uma derivada, vamos derivar o valor do fluxo magnético em relação ao tempo
Passo 5
Finalmente chegamos no ultimo item, calcular o valor numérico da fem com os dados do exercício. Bom, basta usar a equação que deduzimos no item (d) e substituir os valores
Lembrando de passar tudo para o SI
O valor de podemos conseguir no Apêndice F do livro.
Fazendo essa continha temos
Resposta
- , na direção e sentido entrando na página.