Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Exercício - Ex. 8

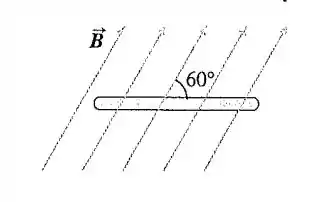
29.8. Uma espira plana e circular de aço, com raio de 75 cm, está em repouso em um campo magnético uniforme, como indica uma perspectiva perpendicular na figura 29.28. O campo varia com o tempo, de acordo com B t = 1,4   T   e - 0,057   s - 1 t . (a) Determine a fem induzida na espira em função do tempo. (b) Quando a fem induzida é igual a 1/10 do seu valor inicial? (c) Determine o sentido da corrente induzida na espira, se observada por cima da espira.

Passo 1

Vamos começar pelo começo, o item (a), podemos calcular o módulo da fem do seguinte modo

ξ i n d = d ϕ B d t

Bom, podemos calcular o fluxo magnético da seguinte forma

ϕ B = A ⋅ B

Mas atente-se na angulação entre o plano da área e o campo magnético, então

ϕ B = A sin ⁡ 60 ° ⋅ B

Logo

ξ i n d = d B ⋅ A sin ⁡ 60 ° d t

ξ i n d = A sin ⁡ 60 °   d B d t

Agora é só substituir o valor do campo magnético, e derivar

d B d t = d d t 1,4   T e - 0,057 s - 1 t

Então

d B d t = 1,4   T ⋅ 0,057   s - 1 ⋅ e - 0,057   s - 1 t

Agora é só substituir os valores

ξ i n d = π r 2 sin ⁡ 60 ° ⋅ 1,4   T ⋅ 0,057   s - 1 ⋅ e - 0,057   s - 1 t

O raio é de 75   c m , ou seja 0,75   m

ξ i n d = π ⋅ 0,75 2 sin ⁡ 60 ° ⋅ 1,4   T ⋅ 0,057   s - 1 ⋅ e - 0,057   s - 1 t

Fazendo essa continha

ξ i n d = 0,12   V e - 0,057   s - 1 t

Passo 2

Agora vamos para o item (b). Vamos calcular o tempo em que a fem tem 1 10 do seu valor inicial, ou seja

ξ = 1 10 ξ 0

Bom o valor inicial ξ 0 é

ξ 0 = 0,12   V

Basta usar a equação que deduzimos no item anterior para t = 0 .

Então

ξ = 1 10 0,12   V

Ou ainda

0,12   V e - 0,057   s - 1 t = 0,12   V 10  

Agora é só isolar o tempo t . Para isso, podemos cortar 0,12   V , e depois passar o l n

ln ⁡ e - 0,057   s - 1 t = ln ⁡ 1 10

Então

- 0,057   s - 1 t = ln ⁡ 1 10

Agora está mais simples isolar o tempo

t = - ln ⁡ 1 10 0,057   s - 1

Fazendo essa continha temos

t = 40,4   s

Passo 3

Agora no item (c) podemos ver que B → esta na direção de A → , então ϕ B é positivo (veja a figura 29.6 do livro). Bom, calculamos também que ξ > 0 , então podemos concluir que a corrente está no sentido anti-horário.

Resposta

  1. ξ i n d = 0,12   V e - 0,057   s - 1 t
  2. t = 40,4   s
  3. Sentido anti-horário
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a seguinte combinação de unidades do SI é equivalente ao volt: T m 2 / s
Um ímã em barra está montado na extremidade de uma mola e oscila em movimento harmônico simples ao longo do eixo de um anel, como mostrado na Figura 28-40. O ímã está em sua posição de equilíbrio quan
Um ímã em barra se move com velocidade constante ao longo do eixo de um anel, como mostrado na Figura 28-39.Faça um gráfico do fluxo magnético através do anel como função do tempo. indique no gráfico
Uma professora de física faz a seguinte demonstração sobre fem. Ela pede para dois estudantes segurarem um longo fio conectado a um voltímetro. O fio é mantido frouxo e forma um grande arco. Quando el
Antes de 1960, as intensidades de campos magnéticos era geralmente medidas por uma bobina giratório gaussimétrica. O dispositivo usa uma pequena bobina com múltiplas voltas girando a uma alta rapidez