Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Exercício - Ex. 29
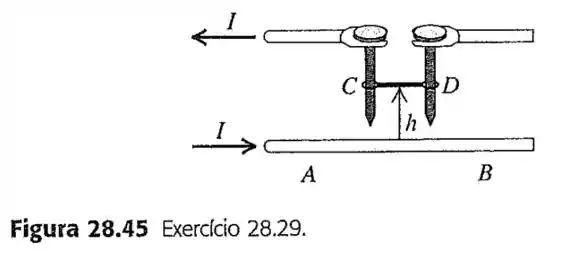
29-Um fio horizontal longo encontra-se apoiado sobre uma mesa e conduz uma corrente . Um fio horizontal longo está verticalmente sobre o fio e pode deslizar para cima ou para baixo ao longo de suas guias metálicas verticais e ( Figura ). O fio está conectado por meio de contatos deslizantes a outro fio que também conduz uma corrente , porém de sentido contrário a corrente do fio . A massa por unidade de comprimento do fio é igual a . Na posição de equilíbrio, qual é a altura do fio , supondo que a força magnética sobre o fio seja inteiramente produzida pela corrente do fio ?
Passo 1
Como visto na questão quando temos correntes de sentido contrários (tal como mostrado na figura) em fios de transmissão paralelos, nós vemos surgir forças magnéticas que tendem a repelir os dois cabos de lugar. Só que o cabo tem uma força peso por conta dos contatos de modo a termos o seguinte diagrama de forças.
Onde a massa por unidade de comprimento do fio vale ou seja:
Onde é o comprimento dos dois fios
E a força magnética em e no fio de baixo:
Onde espero que a essa altura que a força em dois fios paralelos seja de:
Passo 2
Igualando as duas forças (pois a força é causado pela presença dos contatos) e como queremos saber só basta estarmos interessados nas forças que atuam em e não no resto:
Como o cabo está em equilíbrio, ela somente sofre interferência do cabo de baixo então a altura será de: