Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Exercício - Ex. 22
22- Duas linhas de transmissão longas e paralelas separadas por uma distância de , carregam correntes de e . Determine todos os locais em que o campo magnético líquido de ambos os fios é igual a zero, caso essas correntes estejam no mesmo sentido e em sentidos contrários.
Passo 1
Caso as correntes estejam no mesmo sentido então as forças magnéticas nos dois fios são de atração então há um ponto no meio desses dois fios onde o campo magnético irá ser nulo, isso pode ser visto pela regra da mão direita .
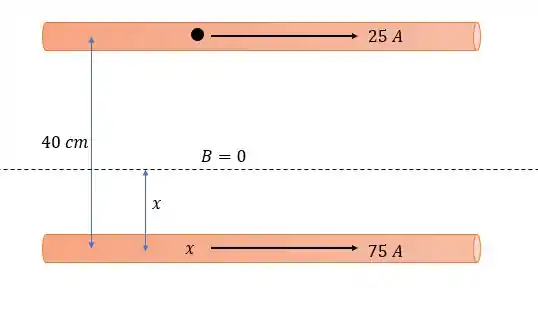
Onde existe uma linha onde o campo magnético é nulo e podemos dizer que ele está a da corrente de , logo igualando os campos magnéticos dos dois fios teremos:
O que nos dá:
Portanto o local onde o campo magnético se zera é a do fio onde corre a corrente de ou a do fio onde corre a corrente de .
Passo 2
Já quando invertemos o sentido de uma das correntes (no caso a de ) nós teremos forças reuplsivas nos cabos e o seguinte comportamento dos campos magnéticos.
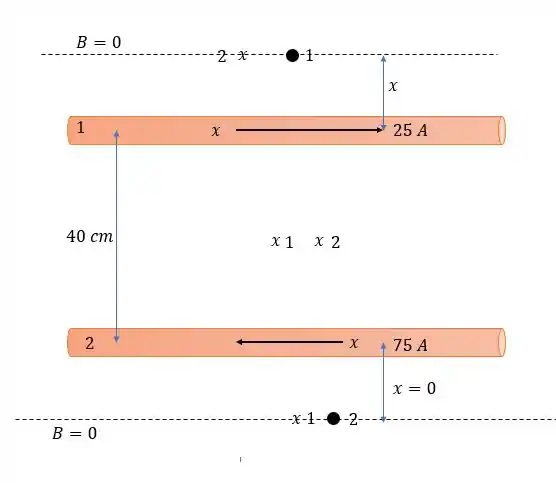
A corrente nos fio e no fio vão produzir um campo magnético entrando na região entre os dois fios , então nunca teremos uma região de campo nulo nessa região. Mas teremos uma região de campo nula tanto acima quanto abaixo dos dois fios, pois o fio 1 produz um campo saindo da folha na região acima dele enquanto o fio 2 produz um campo entrando. E a situação se inverte abaixo do fio 2, logo para a região acima do fio 1 teremos a seguinte situação:
Então a aicma fio de ou a acima do fio de nós temos uma região de campo mangético nula.
Agora a região abaixo do fio de nós temos:
O que nos dá o mesmo resultado do caso anterior então não tem nenhuma região abaixo do fio de que nos dê campo magnético nulo.