Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 35
35. Um trenó de madeira é puxado para cima, por uma corda, sobre a lateral de uma colina com de inclinação e coberta de neve. Um caixote de madeira de encontra-se sobre o trenó. Se a tensão na corda aumentar constantemente, para que valor de tensão o caixote
começará a escorregar?
Passo 1
Então pessoal a base que precisamos para resolver esse problema é a segunda e a terceira lei de Newton, mas para sabermos como usá-las bem, vamos montar um diagrama de corpo livre para o caixote e para o trenó onde teremos nosso eixo paralelo a colina e o eixo perpendicular, temos o seguinte:
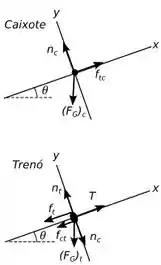
Agora vamos analisar a nossa situação junto com o diagrama para ver os pares de ação e reação que temos presentes.
Temos que a força de atrito (força de atrito que o trenó faz em na caixa) forma um par com a força (força de atrito que a caixa faz no trenó), além desse par temos referente a normal do caixote () causada pelo contato com o trenó, logo teremos uma reação igual e de sentido contrário no trenó, como mostra o diagrama.
Para encontrarmos a maior tensão para que o caixote começa a escorregar, temos que saber a máxima aceleração que o caixote consegue chegar considerando a força de atrito estático máximo entre ele o trenó.
Como você pode ver teremos que usar a força de atrito, para isso precisamos dos coeficientes de atrito estático entre o caixote e o trenó (madeira com madeira) e o coeficiente de atrito cinético entre o trenó e a neve (madeira com neve).
Segundo a tabela do livro temos que que o coeficiente de atrito estático de madeira com madeira é e o atrito cinético de madeira sobre neve é .
E podemos encontrar essa aceleração através da segunda lei de Newton para analisar as forças do caixote, tendo essa aceleração podemos usar também a segunda lei para analisar o trenó e encontrar a tensão que temos para essa máxima aceleração.
Infelizmente nosso enunciado está faltando informação referente a massa do trenó, que deve ter se perdido devido a tradução, mas para manter ele com igual a versão original vamos usar a massa do trenó igual a .
Passo 2
Primeiro vamos analisar o bloco na direção , temos o seguinte:
Agora vamos analisar o caixote na direção , temos:
Usando a expressão da força de atrito temos:
Agora usando que encontramos para e isolando , temos:
Agora substituindo os valores que conhecemos, temos:
Então temos que:
Pronto, encontramos a aceleração que precisávamos.
Passo 3
Agora vamos analisar o trenó, vamos começar com a direção , temos:
Usando a expressão que temos para temos:
Substituindo os valores que conhecemos, temos:
Então temos:
Agora vamos analisar o trenó na direção , temos o seguinte:
Usando a expressão da força de atrito temos:
Substituindo as expressões que temos para e , temos:
Agora vamos isolar e substituir os valores que temos, assim:
Assim temos que: