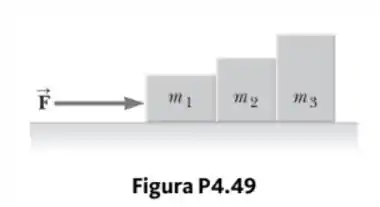
No Exemplo 4.5, empurramos dois blocos sobre uma mesa. Considere que três blocos estão em contato um com o outro sobre uma superfície horizontal sem atrito, como mostrado na Figura P4.49. Uma força horizontal é aplicada a . Seja , , e .
- Desenhe um diagrama de corpo livre separado para cada bloco.
- Determine a aceleração dos blocos.
- Encontre a força resultante em cada bloco.
- Encontre o módulo das forças de contato entre os blocos.
- Você está trabalhando em um projeto de construção. Outro trabalhador está pregando um painel de gesso em um lado de uma parede divisória leve e você está do lado oposto, dando “suporte” ao apoiar as costas contra a parede, empurrando-a. A cada golpe do martelo você sente uma dor nas costas. O supervisor o ajuda a colocar um bloco pesado de madeira entre a parede e suas costas. Usando a situação analisada nas partes (a) a (d) como modelo, explique como essa mudança funciona para tornar seu trabalho mais confortável.
Passo 1
E aiii galera,
Vamos fazer mais uma questão?
Bora lá!
Letra a:
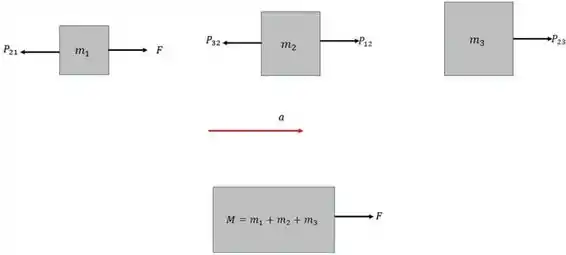
A seguir, os diagramas de corpo livre:
Passo 2
Letra b:
Aplicando a segunda lei de Newton no sistema de todos os blocos. Nós temos:
Passo 3
Letra c:
Usando a segunda lei de Newton, podemos obter a força resultante da seguinte forma:
Para o primeiro bloco:
Para o segundo bloco:
Para o terceiro bloco:
Passo 4
Letra d:
No primeiro bloco:
Como,:
No segundo bloco:
Passo 5
Letra e:
Podemos imaginar minhas costas no lugar do terceiro bloco na situação acima. Como descobrimos na parte (d), a força que atua no primeiro bloco F é maior do que o do segundo bloco e maior do que o do terceiro . Então, colocar um bloco de madeira entre mim e a parede irá reduzir a força alcançando minhas costas.
Resposta
- Ver diagrama
- Podemos imaginar minhas costas no lugar do terceiro bloco na situação acima. Como descobrimos na parte (d), a força que atua no primeiro bloco F é maior do que o do segundo bloco e maior do que o do terceiro . Então, colocar um bloco de madeira entre mim e a parede irá reduzir a força alcançando minhas costas.