Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 34
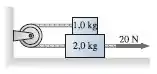
34. O bloco inferior da FIGURA P7.34 é puxado por uma força de tensão de . O coeficiente de atrito cinético entre o bloco inferior e a superfície vale . O coeficiente de atrito cinético entre os dois blocos também vale . Quanto vale a aceleração do bloco de ?
Passo 1
Então pessoal a base que precisamos para resolver esse problema é a segunda e a terceira lei de Newton, mas para sabermos como usá-las bem, vamos montar um diagrama de corpo livre para cada bloco do nosso sistema, temos o seguinte:
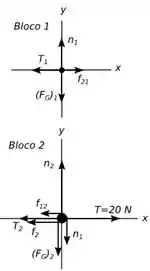
Vamos nos referir ao bloco de cima como bloco e o de baixo como bloco .
Agora vamos analisar a nossa situação junto com o diagrama para ver os pares de ação e reação que temos presentes.
Temos que a força de atrito (força de atrito que faz em ) forma um par com a força (força de atrito que faz em ), além desse par temos referente a normal do bloco () causada pelo contato com , logo teremos uma reação igual e de sentido contrário em , como mostra o diagrama e por último temos que já que a corda que liga os blocos e a polia são ideias.
Então como essa corda que liga os blocos é ideal teremos que a aceleração de , eles têm a mesma aceleração, mas em sentidos diferentes.
Com esses detalhes podemos usar a segunda lei de Newton para analisar a força resultante nos blocos nas direções e e encontrar o que queremos.
Passo 2
Primeiro vamos analisar o bloco na direção , temos o seguinte:
Usando a expressão da força de atrito temos:
Agora vamos analisar o mesmo bloco na direção , temos o seguinte:
Substituindo o que encontramos agora na expressão mais acima, temos:
Passo 3
Agora vamos analisar o bloco , vamos começar com a direção , temos o seguinte:
Substituindo pela expressão que encontramos no passo anterior temos:
Agora vamos analisar o mesmo bloco na direção , temos:
Substituindo as expressões das forças de atrito temos:
Substituindo as expressões de e que conhecemos ficamos com:
Dando uma arrumada ficamos com o seguinte:
Passo 4
Agora vamos pegar a expressão que encontramos no passo anterior e isolar que é o que queremos saber, temos:
Substituindo os valores que conhecemos, temos:
Então temos que: