Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 37
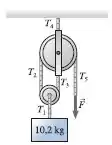
37. O bloco de da FIGURA P7.37 é mantido em repouso pela corda sem massa que passa por duas polias sem massa e livres de atrito. Determine os valores das tensões de a e o módulo da força .
Passo 1
Então pessoal a base que precisamos para resolver esse problema é a segunda e a terceira lei de Newton, mas para sabermos como usá-las bem, vamos montar um diagrama de corpo livre para cada componente do nosso sistema, temos o seguinte:
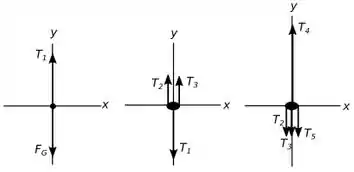
Agora vamos analisar a nossa situação junto com o diagrama para ver se temos forças iguais presentes.
Dessa situação e da propriedade das polias ideias podemos dizer que a tração é igual tração já que eles estão ligados pela mesma corda sem massa e que a tração pelo mesmo argumento anterior.
Vamos então analisar as forças nos elementos do nosso sistema.
Passo 2
Vamos começar analisando a massa , temos o seguinte:
Assim temos que:
Substituindo os valores que conhecemos, temos:
Passo 3
Agora vamos analisar a polia menor, temos:
Sabemos que , assim:
Substituindo o valor , temos:
Então temos que e temos que , já que .
Passo 4
Agora vamos analisar a polia maior, temos:
Substituindo o que sabemos, temos: