Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 38.Exercícios - Ex. 19

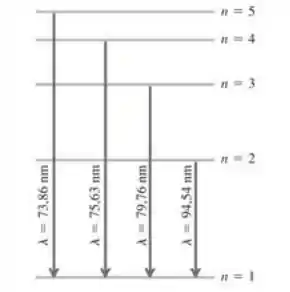
38.19. Em uma série de experiências com um átomo hipotético de um elétron, você mede os comprimentos de onda dos fótons emitidos nas transições que terminam no nível fundamental (n=1), como mostra o diagrama de níveis de energia da Figura 38.37. Você também observa que são necessários 17,5 eV para ionizar esse átomo. A) Qual é a energia do átomo em cada um dos níveis (n=1, n=2 etc.) mostrados na figura? B) Se um eletron fez uma transição do nível n=4 para o nível n=2, que comprimento de onda de luz ele emitiria?

Passo 1

Temos que começar calculando a energia do átomo para cada um dos níveis. Sabemos o seguinte

Δ E = h c λ

Ou seja, a diferença de energia de um nível para o outro depende do comprimento de onda.

Veja, a gente sabe pelo enunciado que

E 1 = - 17,5   e V

Já que a energia de transição do nível mais perto da superfície para fora do átomo é 0 . Como a energia para ionização é 17,5   e V , então E 1 = - 17,5   e V

E para transição n = 5 → 1 :

E 5 - E 1 = h c λ

Então

E 5 + 17,5 = 6,63 ⋅ 10 - 34 1,602 ⋅ 10 - 19   ⋅ 2,998 ⋅ 10 8 73,86 ⋅ 10 - 9

Fazendo essa conta

E 5 = 16,79 - 17,5 = - 0,71   e V

Repara que a gente tem que colocar a constante de Planck em e V ⋅ s

Agora vamos usar o mesmo raciocínio para calcular os outros níveis. Vamos fazer para n = 4 → 1

E 4 - E 1 = h c λ

Então

E 4 + 17,5 = 6,63 ⋅ 10 - 34 1,602 ⋅ 10 - 19   ⋅ 2,998 ⋅ 10 8 75,63 ⋅ 10 - 9

Fazendo essa conta

E 4 = 16 , 40 - 17,5 = - 1,1   e V

Agora vamos fazer n = 3 → 1

E 3 - E 1 = h c λ

Então

E 3 + 17,5 = 6,63 ⋅ 10 - 34 1,602 ⋅ 10 - 19   ⋅ 2,998 ⋅ 10 8 7 9,76 ⋅ 10 - 9

Fazendo essa conta

E 3 = 15,56 - 17,5 = - 1 , 94   e V

E finalmente n = 2 → 1

E 2 - E 1 = h c λ

Então

E 2 + 17,5 = 6,63 ⋅ 10 - 34 1,602 ⋅ 10 - 19   ⋅ 2,998 ⋅ 10 8 94,54 ⋅ 10 - 9

Fazendo essa conta

E 2 = 13,12 - 17,5 = - 4,38   e V

Pronto, temos a energia de todas as camadas:

E 1 = - 17,5   e V E 2 = - 4,38   e V E 3 = - 1,94   e V E 4 = - 1,1   e V E 5 = - 0,71   e V

Passo 2

Agora vamos para o item (b). Temos que calcular o comprimento de onda de uma transição. Bom, podemos usar a mesma equação que estávamos usando no passo anterior. O enunciado descreve o caso onde n = 4 → 2 . Então

E 4 - E 2 = h c λ

Então

λ = h c E 4 - E 2

Agora é só substituir os valores

λ = 6,63 ⋅ 10 - 34 1,602 ⋅ 10 - 19   ⋅ 2,998 ⋅ 10 8 - 1,1 + 4,38

E isso vai dar

λ = 378   n m

Resposta

  1. E 1 = - 17,5   e V E 2 = - 4,38   e V E 3 = - 1,94   e V E 4 = - 1,1   e V E 5 = - 0,71   e V
  2. 378   n m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A frequência de vibração para a molécula de H F é igual a 1,24 × 10 14 H z . O átomo de hidrogênio possui massa igual a 1,67 × 10 - 27 k g e a massa do átomo de flúor é igual a 3,5 × 10 - 26 k g .Qual
Os níveis de energia de rotação para a molécula C O calculados no exercício 42.2 e as diferenças dos níveis de energia de vibração foram dados no exemplo 42.3 . As energias de vibração-rotação são dad
Se a molécula de cloreto de sódio (NaCl) pudesse sofrer uma transição de vibração n → n - 1 sem nenhuma variação do numero quântico de rotação, um fóton com um comprimento de onda igual a 10 μ m seria
Dois átomos de césio (Cs) podem formar uma molécula de C s 2 . A distancia de equilíbrio entre os dois núcleos da molécula de C s 2 é igual a 0,447 nm. Calcule o momento de inercia em relação a um eix
No exemplo 42.2, o momento de inercia para o CO foi calculado usando a Equação (42.6). a) No CO, a que distancia cada átomo fica do centro de massa da moeluca? b) Use I = m 1 r 1 2 + m 2 r 2 para calc