44- Variação no campo magnético. Você está testando um novo sistema de captura de dados. Esse sistema permite registrar um gráfico da corrente em um circuito em função do tempo. Como parte do teste, você usa um circuito composto por um raio de e uma bobina com espiras de fio de cobre conectada em série a um resistor de .

O cobre possui resistividade , e o fio usado para a bobina tem diâmetro de . Você coloca a bobina sobre uma mesa que está inclinada a um ângulo de em relação ao plano horizontal e que fica entre os pólos de um eletroímã. O eletroímã gera um campo magnético verticalmente de baixo para cima que é igual a zero para , igual a para e igual a para .

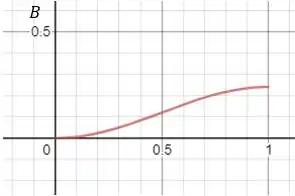
Desenhe o gráfico que deve ser produzido pelo seu sistema de captura de dados. (Trata-se de um sistema completo, portanto o gráfico incluirá classificações e valores numéricos nos seus eixos.)

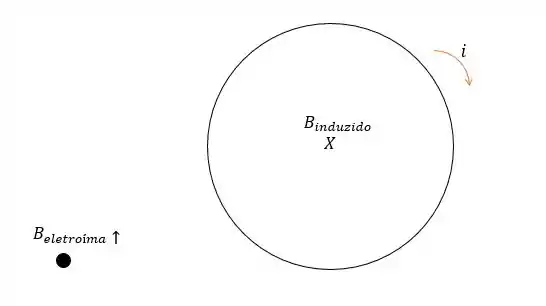
Para quem olha verticalmente de cima para baixo para a bobina, a corrente fluirá no sentido horário ou anti-horário?

Porém esse aparelho de medição é um aparelho de corrente e para isso precisaremos calcular a resistência nesse circuito e que será dada por:

Onde , como o nome tenta dizer, é a resistência do enrolamento e que será calculado por:

Onde é a área transversal do fio , que é um círculo de diâmetro ou um raio de .

Logo a resistência total será de:

Então a corrente terá um gráfico igual a:

Cujo gráfico será (em radianos!):

Se você olha de cima para baixo para as espiras da bobina isso significa que o campo magnético gerado pelo eletroímã está entrando no seu olho, e por estar aumentando no período de , então isso significa que o campo induzido no fio está no sentido de sair do seu olho. Por conta disso o sentido da corrente é no sentido horário.