Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Problemas - Ex. 45

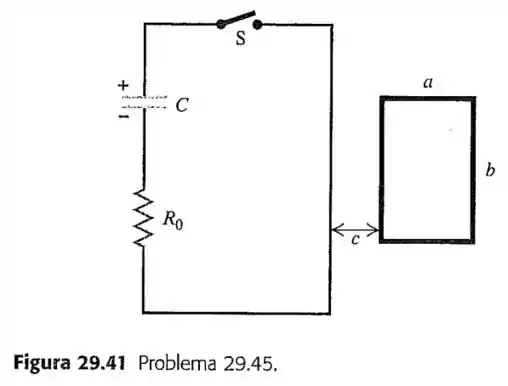
45- No circuito indicado na Figura 29.41 , o capacitor possui capacitância C = 20   μ F e carga inicial de 100   V , com a polaridade indicada. O resistor R 0 possui resistência de 10   Ω . No instante t = 0 , a chave é fechada. O pequeno circuito não está conectado de forma alguma ao maior. O fio do circuito pequeno possui uma resistência de 1.0   Ω / m e contém 25   e s p i r a s .

O circuito maior é um retângulo de 2.0   m por 4.0   m , enquanto o menor possui dimensões de a = 10.0   c m e b = 20.0   c m . A distância c é igual a 5.0   c m . (A figura não está em escala.) Ambos os circuitos são mantidos estáticos. Suponha que somente o fio mais próximo do circuito pequeno produza um campo magnético considerável através dele.

( a ) Determine a corrente no circuito maior 200   μ s após ser fechada.

( b ) Determine a corrente no circuito pequeno 200   μ s após S ser fechada. (Sugestão: veja o Problema 29.7 ).

( c ) Ache o sentido da corrente no circuito pequeno

( d ) Justifique por que podemos ignorar o campo magnético de todos os fios do circuito maior, exceto o do fio mais próximo do circuito pequeno

Passo 1

Esse será um longo problema, então para começar aqui vamos começar escrevendo a resistência no circuito menor, que será de:

R m e n o r = 25 × 2 × 0.1 + 2 × 0.2 × 1 = 15   Ω

Entenda essas 25 espiras, como 25 retângulos como esse um em cima do outro.

E a corrente no circuito R C é dado por :

i t = V R 0 e - t R 0 C

Então a corrente para t = 200 × 10 - 6   s para V = 100 e R 0 = 10   Ω e C = 20 × 10 - 6   F será:

i = 100 10 e - 200 × 10 - 6 10 × 20 × 10 - 6 = 3.679   A

E essa corrente diminuirá a medida que o tempo passa.

Passo 2

O fio mais próximo por estar mais próximo ao menor circuito acaba transferindo todo o campo magnético do circuito maior para o menor (pois está a 5.0   c m do circuito diferente de 2   m , que produzirá um campo bem ridículo perto do fio que está somente a 5   c m ) então o fluxo magnético nessa área será igual a:

d ϕ B = μ 0 I 2 π x   b   d x

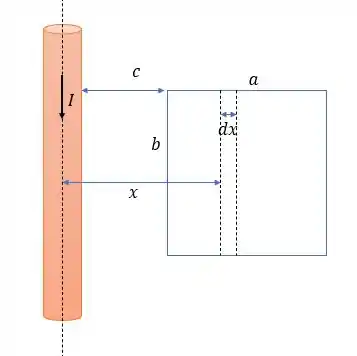
Pois o campo magnético varia na horizontal de c até c + a e ela afeta na área do circuito menor de maneira não uniforme. E I é a corrente no circuito menor.

ϕ B = ∫ c c + a μ 0 I 2 π x   b   d x = μ 0 I 2 π   b l n x c c + a

Então o fluxo magnético nesse circuito menor será:

ϕ B = μ 0 I 2 π ln ⁡ c + a c

Então a fem induzida será de:

ϵ = - N d ϕ B d t

Onde o único termo que pode varia no fluxo magnético é a corrente I , logo:

ϵ = - N μ 0 b 2 π ln ⁡ c + a c d I d t

Onde d I d t = 3.679 200 × 10 - 6 , então substituindo os valores dados nós teremos:

ϵ = - 25 × 4 π × 10 - 7 × 20 × 10 - 2 2 π ln ⁡ 15 5 × 3.679 200 × 10 - 6 = 20.2   m V

Agora finalmente respondendo a letra b temos que a corrente no circuito menor nesse tempo será de:

I = V R = 20.2 × 10 - 3 15 = 1.35   m A

Passo 3

A corrente no circuito maior sai no polo positivo do capacitor, e por isso ela segue o sentido horário no circuito maior, isso faz com que seja produzido um campo magnético que sai da folha do papel na área do circuito menor, e como essa corrente está diminuindo (pela fórmula da corrente de descarga no passo 1) temos que pela lei de Lenz o circuito menor irá responder de forma a manter esse campo magnético saindo da folha no centro dela, então a corrente que passa sobre ela é no sentido anti-horário.

Resposta

a )   3.679   V

b )   1.35   m A

c )   s e n t i d o   a n t i - h o r á r i o

d )   P o r   e s t a r e m   m u i t o   d i s t a n t e s   e m   r e l a ç ã o   a   d i s t â n c i a   c ,   p o d e n d o   s e r   i g n o r a d a s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o fluxo magnético através de um solenoide de 800 voltas que tem comprimento igual a 30,0c m , raio igual a 1,00c m e conduz uma corrente de 2,00 A .
Um condutor cilíndrico longo com raio R e comprimento L conduz uma corrente I . Determine o fluxo magnético por unidade de comprimento através da área indicada na Figura 28-44.
Um longo solenoide tem n voltas por unidade de comprimento, raio R 1 e conduz uma corrente I . Uma bobina circular de raio R 2 e com N voltas é coaxial ao solenoide e está equidistante de suas extremi
Uma bobina circular tem 15,0 voltas, raio de 4,0c m e está em um campo magnético uniforme de 4,0k G na direção + x . Determine o fluxo através da bobina quando a normal unitária do plano da bobina é a
Determine o fluxo magnético através de um solenoide de 400 voltas que tem comprimento igual a 25,0c m , raio igual a 1,00c m e conduz uma corrente de 3,00 A .