Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Problemas - Ex. 50
50- Suponha que a espira da Figura seja
girada em torno do eixo
girada em torno do eixo
girada em torno de um lado da espira paralelo ao eixo
Qual é a fem induzida máxima em cada um desses casos, considerando e ?
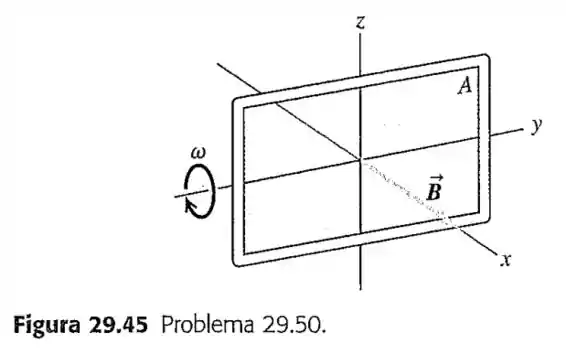
Passo 1
A figura está meio ruim, mas o campo magnético está orientada em e para que haja fluxo magnético a área e o campo magnético devem estar variando em eixos diferentes, e na letra essa área gira em , não variando sua área em então para a letra :
Agora para as letras e a área varia em um eixo perpendicular ao campo magnético nos dando um fluxo magnético variável igual a:
E que variam de forma igual e terão valores de pico iguais a:
Resposta
Exercícios de Livros Relacionados
Quando a corrente em uma bobina de 8 H é igual a 3 A e aumenta para 200 A / s , determine a O fluxo magnético através da bobina e ( b ) a força eletromotriz induzida na bobina.
Um campo magnético com intensidade de 0,200 T está na direção + x . Uma bobina quadrada tem lados com 5,00c m de comprimento e uma única volta que faz um ângulo θ com o eixo z , como mostra a figura 2
Um campo magnético uniforme B → é perpendicular à base de um hemisfério de raio R . Calcule o fluxo magnético (em termos de B e R ) através da superfície esférica do hemisfério.
Um campo magnético de 1,2 T é perpendicular ao plano de uma bobina quadrada de 14 voltas com lados de 5,0c m de comprimento. a Determine o fluxo magnético através da bobina. b Determine o fluxo magnét
Uma bobina circular tem 25 voltas e raio de 5,0 c m . Ela está no equador, onde o campo magnético da Terra é 0,70 G , apontando para o norte. O eixo da bobina é a linha que passa pelo seu centro e é p