Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 45
45. Uma bola de massa , presa a extremidade de um cordão, move-se em um círculo vertical com energia mecânica contante . Qual a diferença entre a tensão na base do círculo e a tensão no topo ?
Passo 1
A seguinte imagem abaixo, representa a bola viajando em um caminho circular com energia constante. foi escolhido para ser zero no ponto mais baixo do círculo e os diagramas de corpo livre sobrepostos mostram as forças que atuam na bola no topo e na base do caminho circular. Vamos aplicar a segunda lei de Newton para a bola na parte superior e inferior do seu caminho para obter uma relação entre e e conservação de energia mecânica para relacionar as velocidades da bola nesses dois locais, que estão sendo requisitados pelo exercício. Consideremos o sistema de análise como o formado pela Terra e pela bola. Desse modo, não há forças externas atuando no nosso sistema e o trabalho das forças externas, , é igual a zero. Mão na massa !
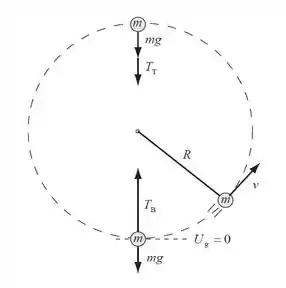
Passo 2
Vamos, primeiro, realizar o procedimento, como descrito no , de aplicar a segunda lei de Newton, considerando a direção radial, para as partes inferior e superior do círculo:
Para o ponto mais baixo:
Temos então que:
E o que é esse ? Bem, o nada mais é do que um velho conhecida da gente. Isso mesmo, o é a aceleração direcionada para o centro do círculo, que popularmente conhecemos pelo nome de aceleração centrípeta e cuja fórmula também já e familiar: a divisão do quadrado da velocidade pelo raio do círculo .Assim a equação anterior passa a ser escrita como:
Para o ponto mais alto:
Em seguida, para o topo, repetimos o mesmo raciocínio. Para esse caso, somam-se as forças e , uma vez que as duas apontas para o centro do círculo.
Obtidas as duas equações que queremos e , agora vamos subtrair a primeira equação da segunda afim de obter alguma relação possível:
Essa equação pelo que parece, não tem um formato nada agradável. Mas quem sabe podemos extrair algo dela, usando o princípio da conservação de energia. Continuemos!
Passo 3
Aplicando o princípio da conservação da energia mecânica para o sistema, que está livre da interferência de forças externas, temos:
Só que não existem forças externas atuando no nosso sistema e o trabalho da força externa é nulo. Consequentemente, considerando as energias potenciais final e inicial ( e e as e energias cinéticas final e inicial ( e ), obtemos que:
Para o instante inicial, considera-se a bola na posição mais baixa e para o final, a bola na posição mais alta. Vamos aos cálculos:
Divide-se tudo por e ficamos com:
Agora sim chegamos a algo! Se for parar pra analisar essa última relação, vemos que há um dado que é comum também a aquela relação lá do , em que terminamos de trabalhar. Logo, basta isolar esse dado e chegar ao resultado que queremos:
Mas, encontramos que . Logo, basta substituir esse termo na expressão de cima e pronto. Conseguimos alcançar o resultado que desejávamos:
Resposta