Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 1.1 - Ex. 58
São dados os seguintes vetores: vale e forma um ângulo de no sentido horário com o eixo e vale e forma um ângulo de no sentido horário com o eixo . (a) Faça um esboço e estime, visualmente a magnitude e o ângulo do vetor tal que resulta em um vetor de magniturde de apontando no sentido . (b) Repita o cáculo da Parte (a) usando o método de componentes e compare seu resultado com a estimativa feita em (a).
Passo 1
a) Oi pessoal, tudo bem? Vamos representar primeiro , e em relação a origem, só para ver a carinha deles
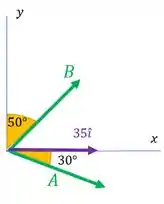
Agora vamos representar essa expressão vetorial:
Que é o mesmo que:
A gente fez essa rearrumação para deixar os vetores conhecidos aparecendo primeiro.
Como fica a representação? A gente vai partir da origem com um vetor com orientação de , mas como o dobro do módulo, para representar . Depois saindo do final de , vamos fazer um vetor igual a , mas no sentido oposto (representando ).
Saindo do início de colocamos o vetor . E saindo do final de e chegando no final de colocamos . Fica assim:
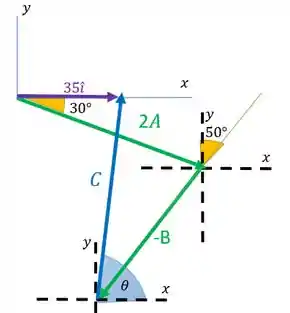
Analisandos somente visualmente, diria que o vetor é maior que o vetor , portanto maior que e possui um ângulo maior que . Diria que seria aproximadamente:
(Aqui é aproximado mesmo, tá? Cê pode avaliar que são outros valores próximos a esses que a gente colocou aqui)
Passo 2
b) Vamos analisar agora por meio dos cálculos. Temos que:
Essa relação vale para as componentes também.
Repara que só aparece na expressão da componente em porque ele está multiplicado pelo vetor unitário .
Isolando as componentes
Passo 3
Precisamos encontrar as componentes de e de
O vetor faz com . Lembrando que entre os eixos e temos , podemos dizer que o ângulo entre esse vetor e o eixo é no sentido anti-horário Aí como esse ângulo está colado em , a componente vai ser o módulo do vetor vezes cosseno:
E em usamos seno
Agora para vamos tentar entender que ângulo esse vetor faz com no sentido anti-horário. Temos que ele faz um ângulo de no sentido horário.
Para achar um ângulo equivalente no sentido anti-horário a outro que está no sentido horário, podemos pegar e tirar o valor do ângulo, no nosso caso, :
Logo, nosso vetor faz com no sentido anti-horário. Aí para achar as componentes fazemos o mesmo que fizemos para . Colocamos cosseno no e seno no :
Passo 4
Substituindo essas componentes na nossas equações e resolvendo:
Agora para
Passo 5
Com isso podemos achar o módulo de
E sua orientação através da fórmulinha:
Resposta
É possível notar que a análise gráfica não fugiu muito da resposta pelos cálculos.