Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 46

46. Obtenha uma expressão para o módulo da força horizontal F da FIGURA P7.46 para a qual m 1 não escorregue para cima nem para baixo sobre a cunha. Todas as superfícies são livres de atrito

Passo 1

A primeira coisa que precisamos fazer é desenhar o diagrama de forças tanto do bloco quando da cunha para que possamos analisar todo o sistema.

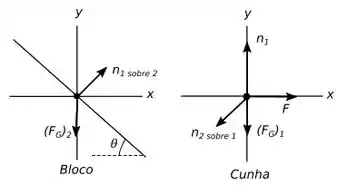
Quando o bloco não escorrega sobre a cunha? Vamos pensar imaginando essa situação.

Quando aplicamos uma força na cunha essa força vai gerar uma aceleração horizontal na cunha. Se o bloco, como o enunciado diz, está livre de atrito ele também possuirá uma aceleração com componente vertical e horizontal.

Agora vamos pensar em duas situações:

  1. Aceleração horizontal da cunha menor que aceleração do bloco.
  2. Aceleração horizontal da cunha maior que a do bloco.

Consegue imaginar o que acontece em cada uma delas?

Na primeira se a aceleração da cunha é menor que a do bloco a velocidade que o bloco vai deslizar é muito maior que a velocidade que a cunha vai se mover e em algum momento o bloco vai tocar o chão. Já na segunda, se a aceleração da cunha for maior que a do bloco a cunha vai ganhar uma velocidade tão superior que vai dar a entender que o bloco foi arremessado para cima.

Ou seja, para que o bloco não escorregue de forma alguma eles precisam possuir a mesma aceleração horizontal.

E a aceleração vertical do bloco? Bom, se olharmos o diagrama de forças do bloco veremos as forças normal e peso atuando. Contudo, é possível ver que se a gente decompor a normal, a componente vertical da normal vai se cancelar com força peso pois a altura do bloco não vai mudar, ou seja, a única força que vai poder gerar uma aceleração será a componente horizontal da normal.

Vendo isso, podemos resolver o exercício.

Passo 2

Como queremos a força horizontal F vamos usar a Segunda Lei de Newton somente com as forças que possuem componentes na direção x na cunha e ver se chegamos no valor de F :

( F r e s ) x = F - n 2   s o b r e   1 s e n   θ = m 1 a → F = m 1 a + n 2   s o b r e   1   s e n   θ

Eita, nós não conhecemos n b   s o b r e   c e nem a mas precisamos deles para achar F . Então vamos dar um jeito de descobrir.

Passo 3

Podemos ver no diagrama de forças que n 2   s o b r e   1 é par ação/reação de n 1   s o b r e   2 , isso significa que sabemos que o módulo da força é igual (apenas o sentido é diferente), ou seja, vamos usar novamente a Segunda Lei de Newton mas agora no bloco para poder descobrir quem é n 1   s o b r e   2 .

( F r e s ) y = n 1   s o b r e   2 cos ⁡ θ - m 2 g = m 2 a

Porém, no Passo 1 eu explico que não tem força pra gerar uma aceleração vertical pois as que existem se cancelam, sendo assim:

n 1   s o b r e   2 cos ⁡ θ - m 2 g = 0   N → n 1   s o b r e   2 =   m 2 g cos ⁡ θ

Achamos n 1   s o b r e   2 , mas falta a então vamos usar mais uma vez a segunda lei mas agora na componente x

( F r e s ) x = n 1   s o b r e   2 sen ⁡ θ = m 2 a → a = n 1   s o b r e   2   s e n   θ m 2 = m 2 g cos ⁡ θ ⋅ s e n   θ m 2 = g tan ⁡ θ

Vamos substituir ele na equação para achar F :

F = m 1 a + n 2   s o b r e   1   s e n   θ = m 1 g tan ⁡ θ + m 2 g cos ⁡ θ   s e n   θ = g tan ⁡ θ   ( m 1 + m 2 )

Resposta

F = g tan ⁡ θ   ( m 1 + m 2 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8 . || A F I G U R AE X 7.8 mostra dois ímãs potentes localizados nas superfícies opostas de uma pequena mesa. A força atrativa de ação a distância entre eles mantém o ímã inferior no lugar. a . Desen
7 . | a . Quanta força faz um astronauta de 80 kg sobre seu assento quando o foguete encontra-se parado na plataforma de lançamento? b . Quanta força faz o astronauta sobre seu assento quando o foguet
21 . || Um cabo de aço maciço com 1,0m de comprimento arrasta um bloco de 20k g sobre uma superfície horizontal livre de atrito. Uma força de 100N exercida sobre o cabo faz com que o bloco percorra 4,
19 . || Em uma caminhada espacial fora da nave, um astronauta de 80k g empurra para longe um satélite de 640k g , exercendo sobre ele uma força de 100N durante a demora de 0,50s para o astronauta esti
9 . || Um carro de 1.000k g empurra um caminhão de 2.000k g cuja bateria descarregou. Quando o motorista pisa no acelerador, as rodas do carro empurram o piso para trás com uma força total de 4.500N .