|| Um cabo de aço maciço com de comprimento arrasta um bloco de sobre uma superfície horizontal livre de atrito. Uma força de exercida sobre o cabo faz com que o bloco percorra em . Desenhe o gráfico da tensão no cabo em função da posição ao longo do cabo, começando no ponto onde o cabo é preso ao bloco.

Com a aceleração calculada anteriormente , achamos a força mínima para mover o bloco, não confunda essa força que vamos calcular agora com a força externa de da corda e nem com a força de tensão. Essa que vamos achar agora é a mínima força necessária para fazer o bloco se movimentar.

Com a força mínima que faz o bloco se movimentar, podemos equacionar uma expressão para um fator da força de tensão aplicada:

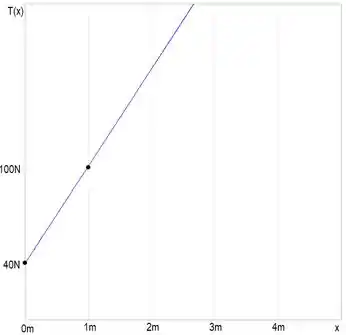
O que achamos foram pontos críticos, nós podemos pensar que o deslocamento ao longo do cabo só ocorrerá se for vencida a e que posteriormente esse deslocamento aumenta linearmente com o . Isso pode ser expresso como uma função de primeiro grau:

O é a posição e é a tensão. O gráfico é mostrado na resposta, foi desconsiderado a parte negativa da posição.