Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 42

42. O bonde mostrado na FIGURA P7.42 desce uma colina de 200   m de altura. Além dos freios, o bonde pode controlar sua velocidade puxando um contrapeso de 1.800   k g que sobe simultaneamente pelo outro lado da colina. O atrito de rolamento sobre o bonde e o contrapeso é desprezível.

  1. De que valor de força de freagem o bonde precisa para descer a rampa com velocidade constante?
  2. Certo dia os freios falham logo após o bonde sair do topo em uma viagem para baixo. Qual será o valor da velocidade do carro ao chegar à base da colina?

Passo 1

PRESTA ATENÇÃO!

Antes de começar toda a resolução do exercício preciso te falar que o enunciado possui um erro. Ele não dar o valor da massa do bonde e esse valor é muito necessário para conseguir as respostas que o exercício quer, então para o exercício ficar compatível com a versão original do livro tenho que dizer pra você que a massa do bonde é de 2000   k g , ok? Agora podemos começar!

Nesse exercício vamos trabalhar com as Leis de Newton então vamos lembrá-las:

Primeira Lei – Um objeto permanecerá em repouso ou continuará movendo-se com velocidade constante (equilíbrio) se e somente se F → r e s = 0 →

Segunda Lei – F → r e s = m a →

Terceira Lei – F → A   s o b r e   B = - F → B   s o b r e   A

Vamos ver também o diagrama de forçar dos dois objetos para facilitar na visão do problema.

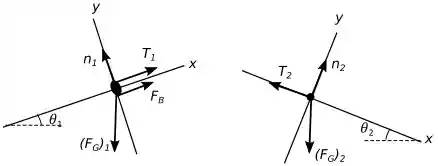
Passo 2

a ) A grande sacada inicial que temos que ter nesse exercício é olhar o diagrama de forças e ver que podemos usar a terceira Lei de Newton de forma muito eficiente.

T 1 é a tração sofrida pelo bonde, já T 2 é a tração sofrida pelo contrapeso, pela terceira lei de Newton sabemos que eles agem como um par de ação/reação. Ou seja:

T 1 = T 2 = T

Esse item fala que o bonde precisa descer com velocidade constante, se a velocidade é constante o sistema está em equilíbrio, de acordo com a primeira lei, sabemos que:

F → r e s = 0   N

Esse item quer a força de frenagem ( F B ) e podemos descobrir usando a segunda lei de Newton para unir essas informações.

Passo 3

Bonde:

F r e s x = T 1 + F B - m 1 g   s e n   θ 1 = 0   N → T = m 1 g   s e n   θ 1 - F B  

F r e s y = n 1 - m 1 g   c o s   θ 1 = 0   N → n 1 = m 1 g   c o s   θ 1

Contrapeso:

F r e s x = m 2 g   s e n   θ 2 - T 2 = 0   N → T   = m 2 g   s e n   θ 2

F r e s y = n 2 - m 2 g   s e n   θ 2 = 0   N → n 2 = m 2 g   s e n   θ 2

Como queremos F B podemos unir as equações das componentes x do bonde e do contrapeso, ou seja:

m 2 g   s e n   θ 2 = m 1 g   s e n   θ 1 - F B → F B = m 1 g   s e n   θ 1 - m 2 g   s e n   θ 2

Substituindo com os valores que temos:

F B = ( 2000   k g ) ( 9,8   m / s ² )   s e n   30 ° - ( 1800   k g ) ( 9,8   m / s ² )   s e n   20 ° = 3766,7   N

Passo 4

b ) Esse item nos avisa que o freio vai falhar, ou seja, aqui temos que considerar que F B = 0   N .

Como não tem freio o bonde vai acelerar de um lado da colina, isso significa que o contrapeso do outro lado da colina também vai acelerar e ambos com a mesma aceleração.

Como o bonde e o contrapeso vão acelerar a força resultante não será mais 0   N . Dito isso, vamos fazer a mesma coisa que no passo anterior.

Bonde:

F r e s x = T + F B - m 1 g   s e n   θ 1 = m 1 a → T = m 1 a + m 1 g   s e n   θ 1

Contrapeso:

F r e s x = m 2 g   s e n   θ 2 - T = m 2 a → T = - m 2 a + m 2 g   s e n   θ 2

Igualando as equações:

m 1 a + m 1 g   s e n   θ 1 = - m 2 a + m 2 g   s e n   θ 2 → -   m 1 g   s e n   θ 1 + m 2 g   s e n   θ 2 = a ( m 1 + m 2 )

Isolando a :

a = - m 1 s e n   θ 1 + m 2   s e n   θ 2 m 1 + m 2 g = - 4,1   m / s ²

Passo 5

Agora que temos a aceleração vamos usá-la na equação de Torricelli e descobrir qual é a velocidade final, ou seja:

v 1 2 = v 0 2 + 2 a ∆ x

Achamos a no passo anterior, sabemos quem é v 0 pois o bonde parte do repouso.

Se a gente definir x 0 = 0 nosso x 1 será dado por:

x 1 = - 200   m s e n   θ 1 = - 400   m

Ou seja:

v 1 2 = 2 ( - 4,1   m / s ² ) ( - 400   m ) → v 1 = 3280   m 2 / s ² = 57,2   m / s

Resposta

a )   F B = 3766,7   N

b )   v 1 = 57,2   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a máquina de Atwood ideal da Figura 4-65. Quando N arruelas são transferidas do lado esquerda para o lado direito, o lado direito desce 47,1c m em 0,40s . Encontre N .
A polia de uma máquina de Atwood ideal recebe uma aceleração a para cima, como mostrado na Figura 4-67. Encontre a aceleração de cada massa e a tensão no fio que as liga. Nesta situação, os dois bloco
Em lugar de realizar a experiência da pg. 69 aplicando a força F através de um esforço muscular, podemos aplicá-la ao disco D de massa m através da força-peso de uma massa m’ suspensa da forma indicad
No sistema de figura, o bloco 1 tem massa de 10 Kg e seu coeficiente de atrito estático com o plano inclinado é de 0,5. Entre que valores mínimo e máximo pode variar a massa m do bloco 2 para que o si
No sistema da figura, m 1 = 20K g ,m 2 = 40K gem 3 = 60K g . Desprezando as massas das polias e dos fios e o atrito, calcule a aceleração do sistema e as tensões nos fios 1,2 e 3.