Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 9.Exercícios e Problemas - Ex. 72
72. Você é um mundialmente famoso advogado-físico que defende um cliente acusado de assassinato. Alega-se que seu cliente, o Sr. Smith, atirou na vítima, o Sr. Wesson. O detetive que examinou a cena do crime encontrou uma segunda bala, que não atingira o Sr Wesson, incrustada em uma poltrona. Você se levanta para interrogar o detetive.
Você: Em que tipo de poltrona a bala foi encontrada?
Detetive: Uma cadeira de madeira.
Você: Qual é a massa da cadeira?
Detetive: Ela tem uma massa de 20 kg.
Você: Como a poltrona respondeu ao ser atingida pela bala?
Detetive: Ela deslizou sobre o piso.
Você: Que distância ela percorreu?
Detetive: Três centímetros. As marcas do deslizamento sobre o piso empoeirado são bem distintas.
Você: De que tipo de piso se trata?
Detetive: Um piso de madeira, feito de tacos de carvalho muito bonitos.
Você: Qual é a massa da bala que você retirou da poltrona?
Detetive: Uma massa de 10 g.
Você: E quanto ela penetrou na madeira?
Detetive: Uma distância de 4 cm.
Você: Você testou a arma encontrada com o Sr Smith?
Detetive: Sim.
Você: E com que valor de velocidade as balas saem do cano dessa arma?
Detetive: Com uma velocidade de 450 m/s.
Você: E qual é o comprimento do cano da arma?
Detetive: A arma tem um cano com 62 cm de comprimento.
Hesitando apenas ligeiramente, você se vira confiantemente para o júri e proclama: “meu cliente não disparou estas balas!”. Como você conseguirá convencer o júri e o juiz disso?
Passo 1
Se liga só! Para facilitar a compreensão do que está acontecendo antes e depois do disparo atingir a vítima.
E aqui embaixo, está nossa bela imagem:
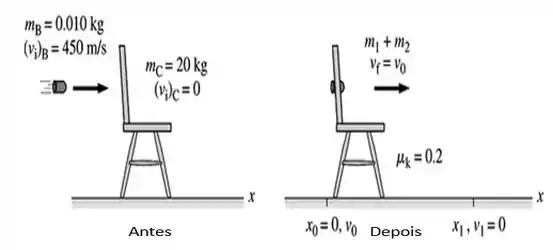
Onde para a nossa cadeira, temos a seguinte imagem abaixo...
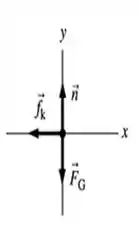
Passo 2
Vamos então, ao nosso argumento:
“Senhoras e senhores do júri, até que ponto a cadeira deslizaria se fosse atingida por uma bala da arma do meu cliente? Sabemos que a velocidade da bala ao sair da arma é de . A bala percorre apenas uma pequena distância até a cadeira, portanto, negligenciaremos qualquer perda de velocidade devido à resistência do ar”.
“A bala e a cadeira podem ser consideradas um sistema isolado durante o breve intervalo da colisão. A bala se encaixou na cadeira, então essa foi uma colisão perfeitamente inelástica”
A conservação do momento, então, permite calcular a velocidade da cadeira imediatamente após a colisão, da seguinte maneira abaixo...
Bem! Chamando de a massa da bala e de a massa da cadeira, ficamos então com...
Isolando e substituindo os valores numéricos...
Continuemos nossa tese...
Passo 3
A velocidade anterior é a velocidade imediatamente após a colisão, quando a cadeira começa a deslizar, mas antes de cobrir qualquer distância.
Para o propósito do problema em dinâmica, chamemos isso de velocidade inicial . O diagrama de corpo livre da cadeira, feito no , mostra três forças.
Desse modo, aplicando a segunda lei de Newton à cadeira (com a bala incorporada), obtemos que...
Como a força normal é dada por...
Então...
Essa vai ser a aceleração responsável por reduzir a velocidade do sistema (cadeira+bala),após a colisão, até que ela venha a valer zero...
Passo 4
Apliquemos assim, a equação de Torricelli...
Sendo que é a velocidade depois da parada total do sistema, no caso . Substituindo os outros valores que temos...
E voilá! Temos finalmente a resposta pro nosso caso!
Se a bala perdesse alguma velocidade no ar antes de bater na cadeira, a distância deslizante seria ainda menor. Assim, pode-se ver que o máximo que a cadeira poderia deslizar se tivesse sido atingida por uma bala da arma do nosso cliente seria de .
Mas, na realidade, a cadeira deslizou , mais do que o dobro. A arma do crime, senhoras e senhores, era uma arma muito mais poderosa do que a que nosso cliente possuía.
Caso encerrado!