Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 9.Problemas - Ex. 16

Qual é o ângulo máximo de espalhamento elástico de uma partícula alfa por um nêutron em repouso?(massa da alfa ∼ 4 x massa do nêutron). Neste ângulo, que fração da energia cinética indicente vai para o nêutron de recuo, e qual é o ângulo entre a direção de recuo e a de incidência?

Passo 1

  1. Falaaa galeraa, animação pra fazer umas continhas? Hehe.

    2. Aqui vamos desenhar um esquema dos momentos lineares após a colisão, saca só

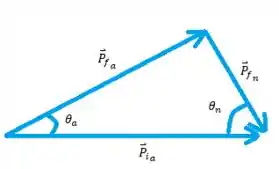
    Bora lá, o momento inicial do sistema é só da partícula alfa e vale P ⃑ i a , pela conservação do momento a soma dos momentos finais P ⃑ f a + P ⃑ f n tem que ser igual ao momento inicial, show!

    Nosso objetivo é encontrar θ a , o ângulo de espalhamento da partícula alfa, pra isso vamos olhar a lei dos cosenos nesse triângulo

    P f n 2 = P i a 2 + P f a 2 - 2 P i a P f a c o s θ a       ( 1 )

    Temos também a conservação de energia cinética do sistema,

    T f = T i

    Vamos escrever em relação aos momentos finais e inicias

    P f n 2 2 m n + P f a 2 2 m a = P i a 2 2 m a

    Reorganizando,

    P f n 2 = 2 m n 2 m a P i a 2 - P f a 2

    Sabemos que a massa da partícula alfa é 4 vezes a do nêutron e por isso m n m a = 1 4 . Nossa equação fica assim

    P f n 2 = 1 4 P i a 2 - P f a 2             ( 2 )

    Substituindo a (2) na (1) agora,

    1 4 P i a 2 - P f a 2 = P i a 2 + P f a 2 - 2 P i a P f a c o s θ a      

    Vamos mexer um pouco pra deixar no formato de equação de segundo grau,

    P f a 2 1 + 1 4 + P f a - 2 P i a c o s θ a + 3 4 P i a 2 = 0  

    Caso tivéssemos informação sobre o momento inicial e o ângulo de espalhamento essa equação só teria solução para   P f a se Δ ≥ 0 , ou seja

    b 2 - 4 a c ≥ 0

    Nesse caso que escrevemos:

  • a = 5 4
  • b =   - 2 P i a c o s θ a
  • c = 3 4 P i a 2

Vamos verficiar a igualdade do delta, saca só como fica

4 P i a 2 cos 2 ⁡ θ a - 4   . 5 4   . 3 4   P i a 2 ≥ 0

→

4 P i a 2 cos 2 ⁡ θ a - 15 16 ≥ 0

Galera, olhando pra ângulos entre 0 ° e 90 ° , na medida em que um ângulo aumenta, seu coseno diminui. Ou seja, existe um ângulo máximo que deixa essa expressão verdadeira, pois caso ele aumente demais cos 2 ⁡ θ a - 15 16 será menor que 0. Vamos escrever, então

cos 2 ⁡ θ a m á x - 15 16 = 0

c o s θ a m á x = 15 16

θ a m á x = a r c o s 15 16 = 14,5 °

Passo 2

  • Nossa fração de energia cinética incidente pode ser escrita assim

    • f = E n e r g i a   n ê u t r o n E n e r g i a   i n i c i a l

    Vamos continuar trabalhando em função dos momentos lineares, fica assim

    f = P f n 2 2 m n P i a 2 2 m a

    f = m a m n P f n 2 P i a 2         ( 3 )

    Daqui nós já sabemos que a razão entre as massa é 4, mas vamos pegar láaa em cima a equação (1) pra substituir P f n 2 . Fica assim

    f = 4 P i a 2 + P f a 2 - 2 P i a P f a c o s θ a P i a 2      

    Dividindo termo a termo ficamos com

    f = 4 1 + P f a P i a 2 - 2 c o s θ a P f a P i a       ( 4 )

    Show! Mas e pra descobrir P f a P i a ? Vamos olhar pra nossa equação do segundo grau lá em cima. Estamos considerando o ângulo em que o Δ = 0 , ou seja, nosso x vale - b 2 a !! Agora sim hein.

    Substituindo os valores de b e a temos

    P f a = - - 2 P i a c o s θ a 10 4

    →

    P f a P i a = 0,8 c o s θ a                 ( 5 )

    Voltando pra equação (4) temos

    f = 4 1 + 0,8 c o s θ a 2 - 2   .   0,8 cos 2 ⁡ θ a      

    = 4 (   1 - 0,96 cos 2 ⁡ 14,5 ° )

    = 0,4

    Passo 3

    Estamos quase lá galera, pra descobrir o ângulo de recuo do nêutron vamos considerar o triângulo que a gente desenhou no começo. Aplicando a lei dos senos nele obtemos o seguinte

    P f n s e n θ a = P f a s e n θ n

    →

    s e n θ n = P f a P f n s e n θ a         ( 6 )

    Nosso desafio agora é achar P f a P f n . Considerando a equação ( 3 )

    f = 4 P f n 2 P i a 2  

    Pra eliminar esse termo de baixo vamos usar a relação (5), então temos

    P i a = P f a 0,8 c o s θ a

    f = 4   .   0,8 2 cos 2 ⁡ θ a P f n P f a 2

    →

    P f n P f a 2 = f 4   .   0,8 2 cos 2 ⁡ θ a

    Invertendo os termos e tirando a raiz dos dois lados,

    P f a P f n = 4   .   0,8 2 cos 2 ⁡ θ a f

    = 4   .   0,8 2 cos 2 ⁡ 14,5 ° 0,4

    = 2,445

    Agora é só voltar para a equação 6 que matamos a questão!

    s e n θ n = 2,445   s e n 14,5 °

    →

    θ n = a r c s e n 0,612

    = 37,7 °        

    Resposta

    a )   14,5 °

    b )   0,4     e   37,7 °

    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    Uma bola de aço de 3,00k g bate em uma parede com velocidade de 1 0,0m / s a um ângulo de θ=60,0 ° com a superfície. Ela quica e recua com a mesma velocidade e mesmo ângulo (Fig. P8.9). Se a bola esti
    Em um jogo de softball, uma bola de 0,200k g cruza a mesa a15,0m / s a um ângulo de 45,0 º º abaixo da horizontal. O batedor bate na bola em direção ao centro do campo, proporcionando uma velocidade d
    Há (pode-se dizer) três teorias igualmente importantes de movimento para uma partícula isolada: a Segunda Lei de Newton, que afirma que a força total sobre a partícula causa sua aceleração; o teorema
    O ângulo descrito por uma unidade de disco girando é dado θ t = a + b t - c t 3 , onde a , b e c são constantes positivas tais que se t for dado em segundos, θ deve ser medido em radianos.Quanto t = 0
    A velocidade angular de um volante obedece à equação ω z t = A + B t 2 , onde t está em segundos e A e B são constantes, com valores numéricos de 2,75( p a r aA ) e 1,5( p a r aB ) . a) Quais são as u